Засоби складання математичних моделей

У ході математичного моделювання об'єктів хімічної технології завжди

потрібно вирішувати три основні задачі:

- побудова математичного опису;

- дослідження математичної моделі;

- прийняття оптимальних рішень.

Під математичним описом розуміє запис закономірностей протікання процесу в об'єкті у вигляді порівнянь, краєвих та початкових умов й логічних зв'язків.

Задача складання математичного опису - сама складна, тонка і відповідальна частина математичного моделювання. При цьому важливо не стільки знання математики, скільки глибоке розуміння сутності протікаючих в об'єкті фiзико-хімічних процесів.

Побудова моделі у загальному випадку включає:

- складання математичного опису;

- рішення порівнянь математичного опису (аналітичне або шляхом

утворення моделюючого алгоритму);

- перевірку адекватності моделі;

- остаточний вибір моделі (при наявності деяких моделей).

Існують три засобу складання математичного опису:

1) Емпiричний (експериментально статистичний, засіб "чорного ящика").

2) Експериментально-аналітичний (феноменологічний).

3) Теоретичний (структурний).

1. 5. 1. Емпiричний засіб

Емпiричний засіб, в основному, використовується, коли процес мало вивчений або нічого невідомо о його природі. Цей засіб також дозволяє отримати математичний опис діючого об'єкту без дослідження його внутрішньої структури.

Зовнішні зв'язки будь-якої системи можна представити у вигляді такої схеми (рис. 1. 2).

Вхідні параметри поділяються на три групи Х - контрольовані, але не регулюємі параметри;

U - контрольовані і регулюємі параметри (керуючі параметри);

Z - неконтрольовані та нерегулюємі параметри (обурення).

Рис. 1. 2

Модель "чорного ящикa" - модель об'єкта, створена безвідносно внутрішніх властивостей об'єкта, без врахування фізичної сутності процесів, що протікають

у ньому. Дaнa модель відобрaжaє зaлежність знaчень вихідних пaрaметрів від вхідних.

Математичний опис у загальному виді становить систему порівнянь виду:

В принципі ці порівняння визначають залежність i-го виходу від всіх

вхідних діянь. Але установити вид функцій F принципово ніяк - адже обурення Z

нам невідомі. Проте, у більшості випадків, кожне з порівнянь можна представити у вигляді

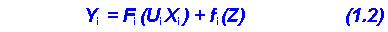
Тут функція розтрощена на дві складові: залежність F від контролюємих параметрів та похибка ("шум ") f. Тепер задача i ставиться таким образом: установити вид функції F_i та оцінити " шум " f_i. Під математичною моделлю будемо розуміти саме Y_i = F_i (U_i, X_i). Це порівняння, що встановлює зв'язок між вихідними та i ії вхідними параметрами, називають порівнянням регресiї. Найбільш часто цю функцію представляють алгебраїчним многочленом.

Звичайно спершу розраховують більш прості многочлени, відхилення досвідчених точок від розрахункових значень порівнюють з випадковою помилкою експерименту. Якщо обидві величини одного порядку, отой опис вважають задовільним. Якщо відхилення не можна пояснити випадковою помилкою, оте розраховують більш складний многочлен. По мірі збільшення порядку многочлена точність опису зростає, але одночасно, по-перше, збільшується необхідне число опитів для знаходження коефіцієнтів многочлена, а, по-друге, ускладнюється трактова моделі.

Порівняння регресiї можна отримати одним з трьох способів:

1. Пасивний експеримент.

2. Активний експеримент.

3. Визначення реакції об'єкту на стандартне обурення.

Пасивний експеримент - виробляється збиранням та аналізом інформації

про стан технологічних параметрів об'єкту без спеціальної зміни вхідних

параметрів процесу.

Достоїнства наданого засобу - практично повністю відсутні витрати на

експеримент.

Недоліки: 1. У нормальних умовах експлуатації вагання технологічного

режиму невеликi і тому експериментальні точки близькi друг до друга. В цих

умовах на точність опису можуть сильно повіяти випадкові помилки.

2. Необхідно мати достатньо велику кількість експериментальних

наданих.

Активний експеримент - складається у цілеспрямованій зміні вхідних

параметрів технологічного процесу. В основі цього засобу лежить планування

експерименту.

Практично всі процеси хімічної технології є складними і на показники

процесу виявляють вплив велике число факторів. Можливі два підходу до дослідження таких многофакторних систем. Перший заснований на отому, що дослідження об'єкту розбивається на серії, в кожної з яких досліджується зміна тільки одного параметра при фіксованих інших. Другий підхід заснований на побудові плану експерименту, що передбачає зміну всіх спливаючих факторів. Такий план повинен забезпечити максимум точності та мінімум кореляції.

Такий експеримент називають многофакторним.

Достоїнством першого підходу є його наочність та простота iнтерпретації результатів, що отримуються. Другий підхід значно ефективнєє - при отому ж обсязі експериментальних досліджень та отієї ж точності опитів отримується

істотно велика точність результатів.

У вигляді прикладу розглянемо вплив температури (x₁), та часу перебування (x₂), на вихід продукту (y₂). Математичну модель отримуємо у виді полiнома 1-й міри лінійного порівняння регресії – y = b + bx + bx. Для цього використовуємо плани 1-го порядку, що будуються наступним чином. Обираємо центр області, що досліджується (центр плану), й у нього переноситься початок координат. Задаються мінімальні (min) та максимальні (max) значення вхідних параметрів х₁ та х₂.. Складаємо план експерименту (рис. 1.3а). При цьому кожний фактор приймає лише два значення - вар'ірується на двох рівнях

(верхньому та нижньому).

На наступному етапі перемінні кодируються. При цьому координати центру

плану прирівнюються до нулю, а інтервали вар'їрування приймають за одиницю. Кодировані перемінні значно полегшують обробку результатів опитів, що в даному випадку проводиться у стандартній формі, не залежній від конкретних умов завдання.

Матрица планування для кодированих перемінних має вид (рис. 1.3б)

Рис. 1. 3а Рис. 1. 3б

На практиці для скорочування запису часто замість " +1 " та " –1 " просто пишуть " + ", " – ". план, що розглядається, побудовам так, що кожний фактор вар'ірується на двох рівнях, причому у опитах перебираються всі можливі комбiнації двох рівней факторів. Такий план називають планом повного факторного експерименту на двох рівнях. Визначимо значення коефіцієнтів по наступним формулам:

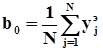
Активний експеримент дозволяє за рахунок цілеспрямованої зміни вхідних параметрів отримувати необхідний обсяг інформації при істотно меншому числі опитів, чим при пасивному експерименті.

При визначення реакції об'єкту на стандартні обурення на вхід подається який-то стандартний сигнал - одиничний iмпульс, східчаста або синусоїдальна зміна вхідного параметра рис. 1.4.

Рис. 1. 4

де t – час;

С_вх – концентрація вхідного компонента

Дослідження об'єкту при нанесенні стандартних обурень помітно полегшує обробку інформації,що одержується. Цим способом в основному користуються при вивченні динаміки (перехідних характеристик) об'єкту, при визначенні гідродинамічних обставин та ін.

При використанні емпiричних засобів математичний опис складається

наступним чином:

1. Проводяться експерименти засобом "чорного ящика ", т. є. вивчається реакція об'єкту на різноманітні обурення.

2. Здійснюється статистична обробка результатів та пошук найкращий форми

апроксимації одержаних даних.

3. Будується математичний опис.

Єдиним критерієм застосування одержаного математичного опису є найвелика простота порівняння при хорошої апроксимації експериментальних даних.

Загальна оцінка експериментальних засобів.

Достоїнства: простота описання доступність одержання моделей можливість побудови моделі за відсутності теорії процесу.

Недоліки: неможливість застосування моделі для режимів, для яких не

проводилися вимірювання; неможливість застосування моделі при переході до

інших установок; неможливість екстраполяцiї результатів.

Дата добавления: 2014-11-18