Графический метод решения

Программирования, графический метод решения

Геометрическая интерпретация задач линейного

В отдельных случаях задачи линейного программирования удается решить с помощью наиболее простого и наглядного геометрического метода. Геометрический метод позволяет наглядно описать область допустимых решений, целевую функцию и процесс получения оптимального решения путем последовательного приближения к оптимальной точке.

Система линейных ограничений задачи (1.5) задает в пространстве многогранное множество – область допустимых решений. Экстремум целевой функции (1.4) достигается на его границе, чаще всего в одной из вершин многогранника.

Если задача зависит от двух переменных x₁ и x₂, то ее можно решить графически. Рассмотрим пример.

Задача 1.4. Найти оптимальный план математической модели:

Z = 2∙x₁+x₂+4 → max

x₁ + x₂ 4

8∙x₁ - 4∙x₂ 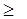-16

x₁ ≤ 2

x₁, x₂ 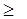0.

РЕШЕНИЕ.

1 П о с т р о е н и е о б л а с т и д о п у с т и м ы х р е ш е н и й.

Последовательно определим области точек, удовлетворяющих каждому ограничению в отдельности. Границами этих областей будут прямые, уравнения которых получаются из ограничений.

Границей допустимой области первого ограничения является прямая

x₁ + x₂ = 4; (1)

границей второго ограничения – прямая

8∙x₁ - 4∙x₂ = -16; (2)

третьего – прямая

x₁ = 2. (3)

Построим эти прямые на чертеже (рисунок 1.1). Для каждого ограничения стрелкой отметим: в какой стороне от граничной прямой располагается допустимая область.

Рисунок 1.1 – Нахождение оптимального плана графическим методом

Например, рассмотрим первое ограничение задачи. Границей его допустимой области является прямая (1). Очевидно, в точках этой прямой выполняется равенство x₁ + x₂ = 4. Чтобы узнать, где расположены точки, удовлетворяющие x₁ + x₂ > 4, подставим в это неравенство координаты любой точки на плоскости, например (0,0). Получим 0+0 > 4 – это неверно, следовательно, все точки, лежащие ниже прямой (1) также не удовлетворяют первому ограничению. Тогда область точек, удовлетворяющих ограничению, будет лежать выше прямой: на что и указывает стрелка.

Пересечением допустимых областей всех ограничений является

Δ АВС, он представляет собой множество допустимых решений задачи.

2 П о с т р о е н и е л и н и и у р о в н я ц е л е в о й ф у н к ц и и

и определение направления ее наискорейшего возрастания

Линия уровня функции определяется уравнением

,

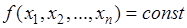т.е. это область точек, в которых функция принимает одно и тоже значение, равное некоторой заданной константе .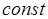

Если функция зависит только от двух переменных и является линейной, ее линия уровня 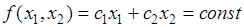представляет собой прямую на плоскости координат .

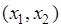Построим линию уровня целевой функции. Константу задаем произвольно, но так, чтобы прямую можно было легко расположить на нашем рисунке 1.1. Если взять 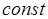= 4, то уравнение линии уровня будет иметь вид:

2∙x₁+x₂ = 0.

Очевидно, эта прямая проходит через начало координат; на рисунке она обозначена Z=4. Нашей задачей является определение такой линии уровня целевой функции, чтобы она соответствовала наибольшему из возможных ее значений в пределах нахождения в допустимой области (Δ АВС).

Линии уровня линейной функции параллельны.

Так как экстремум целевой функции достигается на границе многоугольника допустимых решений, оптимальную точку определяем параллельным перемещением прямой 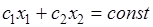в направлении возрастания (при поиске максимума) или убывания (в задачах минимизации) вплоть до крайней точки допустимой области.

Направление наискорейшего возрастания функции определяет ее градиент: вектор с координатами (с₁, с₂), перпендикулярный линии уровня. На рисунке 1.1 показан градиент 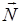целевой функции Z = 2∙x₁+x₂+4, с координатами (2, 1).

3 О п р е д е л е н и е о п т и м а л ь н о г о п л а н а

Перемещаем линию уровня Z=4 параллельно в направлении градиента 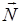. По ходу движения целевая функции возрастает. Очевидно, для того, чтобы выполнялись ограничения задачи, перемещаемая прямая должна иметь хотя бы одну общую точку с допустимой областью (Δ АВС). Таким образом, оптимальной точкой является вершина В. Через эту точку проходит линия уровня Z=Z_МАХ, в точках которой целевая функция принимает значение Z_МАХ. Координаты вершины В являются решением системы уравнений, составленной из уравнений пересекающихся прямых (2) и (3):

.

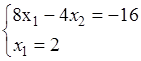Оптимальный план:

, ,

Z_МАХ = 2∙x₁+x₂+4 =2∙2+8+4 = 16.

Дата добавления: 2014-11-18