Симплекс-метод с искусственным базисом

Если математическая модель задачи линейного программирования содержит неравенства со знаком «≥» или (и) «=», для ее решения следует использовать симплекс-метод с искусственным базисом. Рассмотрим решение следующей задачи.

Задача 2.2. Определить оптимальный план задачи линейного программирования:

max Z = 25 x₁ + 50 x₂ + 40 x₃

25 x₁ + 50 x₂ ³ 21000

40 x₃ ³ 12000

x₁ + x₂ + x₃ 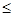1000

10 x₁ + x₂ +25 x₃ 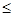15760

x_1, x_2, x₃ ³0

Вначале запишем задачу в каноническом виде, путем введения дополнительных и искусственных переменных. С помощью этих переменных система неравенств принимает вид уравнений.

Если в неравенстве стоит знак 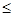, то к левой части этого неравенства прибавляется некоторая неизвестная неотрицательная величина – дополнительная переменная. Ее обозначают буквой x с соответствующим номером.

Если в неравенстве стоит знак ³, то от левой его части вычитается дополнительная неотрицательная переменная. Кроме того, в такие ограничения вводятся искусственные переменные, которые служат для создания опорного решения.

Искусственные переменные вводятся также в целевую функцию с коэффициентом «–М» при решении задачи максимизации и с коэффициентом «+М» при минимизации целевой функции, где М – положительная константа, превосходящая модуль любого из коэффициентов целевой функции.

В результате получаем задачу в каноническойформе:

z = 25 x₁ + 50 x₂ + 40 x₃ + 0·()- M x₈ - M x₉ ® max

25 x₁ +50 x₂ – x₄ + x₈ = 21000

40 x₃ - x₅ +x₉ = 12000

x₁ + x₂ + x₃ + x₆ =100

10 x₁ + x₂ + 25x₃+ x₇ =15760

x_J ³0,j=1,2,…,9

В симплекс-методе с искусственным базисом первоначальная таблица имеет две последние строки «М+1» и «М+2». Строку «М+1» формируют аналогично симметричному симплекс-методу, а в строку «М+2» записывают суммы соответствующих коэффициентов ограничений с искусственными переменными. В нашей задаче – это коэффициенты первого и второго ограничений. Сегмент последних двух строк, принадлежащий столбцам искусственных переменных x₈ и x₉, заполняют нулями.

Выпишем первую симплексную таблицу.

Таблица 1 – Первоначальная симплексная таблица.

Базис

B

X₁

X₂

X₃

X₄

X₅

X₆

X₇

X₈

X₉

X₈

-1

X₉

-1

X₆

X₇

М+1

-25

-50

-40

M+2

Разрешающий столбец определяют по наибольшему положительному элементу строки «М+2». Разрешающую строку выбирают по тому же правилу, что и в симплекс-методе без искусственных переменных. В ходе итераций искусственные переменные вытесняются из базиса, а соответствующие им столбцы исключают. Процесс продолжается до тех пор, пока все коэффициенты строки «М+2» не станут равными нулю. На этом первый этап решения задачи завершается. Его результатом является опорный план исходной задачи. Далее используются алгоритм симплекс-метода с выбором разрешающего столбца по строке «М+1».

В таблице 1 разрешающий элемент находится в строке 1 столбца х ₂. В результате пересчета получим таблицу 2.

Таблица 2 – Вторая симплексная таблица

Базис

B

X₁

X₂

X₃

X₄

X₅

X₆

X₇

X₉

X₂

0.5

0.020

X₉

-1

X₆

0.50

0.02

X₇

9.5

0.02

М+1

-21000

-40

-1

M+2

Разрешающий элемент находится в строке 2 столбца х ₃. Следующая таблица будет иметь вид:

Таблица 3 – Третья симплексная таблица

Базис

B

X₁

X₂

X₃

X₄

X₅

X₆

X₇

X₂

0.5

-0.02

X₃

-0.03

X₆

0.5

0.02

0.03

X₇

9.5

0.02

0.63

М+1

-1

-1

М+2

В таблице 3 нет столбцов x₈ и x_9, так как эти искусственные переменные исключены из базиса. Строку «M+2» следует отбросить. Завершен первый этап решения задачи.

Разрешающий элемент находится в строке 3 столбца х₄.

Таблица 4 – Четвертая симплексная таблица

Базис	B	X1	X2	X3	X4	X5	X6	X7
X2						0.02
X3						-0.03
X4						1.25
X7						0.60	-1
M+1						0.25

Последняя строка таблицы 4 не содержит отрицательных элементов, следовательно, выполнился критерий оптимальности. Завершен второй этап решения.

Оптимальный план:

, , , ,

, ,

.

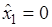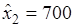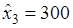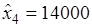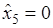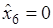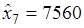
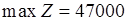Дата добавления: 2014-11-18