Теоремы двойственности в линейном программировании

Понятие о двойственных задачах

ПРОГРАММИРОВАНИЯ

ДВОЙСТВЕННЫЕ ЗАДАЧИ ЛИНЕЙНОГО

Контрольные вопросы к разделу 2

1. Чем каноническая форма задачи отличается от исходной модели линейного программирования?

2. В каких случаях для решения задачи симплекс-методом в ограничения вводятся дополнительные переменные? дополнительные и искусственные переменные?

3. При выполнении каких условий итерационный процесс нахождения оптимального плана симплекс-методом завершается?

4. Каков экономический смысл дополнительных переменных в ресурсных ограничениях задачи линейного программирования?

5.С какими коэффициентами вводятся в целевую функцию искусственные переменных в задачах минимизации? максимизации?

6 Как по последней симплекс-таблице определить максимально возможное увеличение дефицитного ресурса при котором ассортимент выпускаемой предприятием продукции не изменится?

7 Как по оптимальному плану, полученному в результате решения задачи симплекс-методом, определить какие ресурсы и в каком количестве остались недоиспользованными?

8 Как по оптимальному плану, полученному в результате решения задачи симплекс-методом, определить виды нерентабельной продукции?

9. Что является признаком завершения первого этапа решения задачи симплекс-методом с искусственными переменными?

10. Что является признаком завершения второго этапа решения задачи симплекс-методом с искусственными переменными?

С каждой задачей линейного программирования можно связать некоторую другую линейную задачу, называемую двойственной. Рассматриваемая задача по отношению к своей двойственной называется исходной или прямой. Рассмотрим пример построения двойственной задачи.

В качестве исходной задачи возьмем задачу производственного планирования. Формулировка ее такова. В распоряжении предприятия имеются 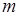видов ресурсов соответственно в количествах, равных b₁, b₂, …, b_m. Эти ресурсы должны быть использованы для производства n видов продукции, стоимость единицы которой известна и равна c_j (j=1,2, …, n). Кроме того, известны нормы a_ij потребления каждого из ресурсов на производство единицы всех видов продукции. План производства 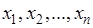следует составить из условия максимизации общей стоимости продукции

(3.1)

при ограничениях на использование ресурсов

(3.2)

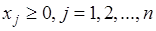. (3.3)

По исходным данным задачи (3.1)-(3.3) сформулируем другую экономическую задачу. Для этого предположим, что нужно решить вопрос о том,

что выгоднее: продать имеющиеся на предприятии ресурсы или произвести из них продукцию согласно оптимальному плану задачи (3.1)-(3.3)? В связи с этим возникает необходимость вычислить оптимальные цены у₁, у₂, …, у_m на эти ресурсы, исходя из следующих соображений:

1) покупатель ресурсов стремится минимизировать их общую стоимость;

2) с другой стороны, предприятие за каждый вид ресурсов желает выручить сумму, не меньшую той, которую оно может получить, произведя из них продукцию.

Приведенная формулировка позволяет получить следующую математическую модель. Минимизировать общую стоимость всех ресурсов

(3.4)

при условиях (стоимость ресурсов, которые следует израсходовать, чтобы выпустить единицу j-й продукции не должна быть меньше цены на эту продукцию)

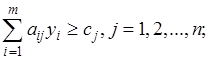(3.5)

. (3.6)

Задача (3.4)-(3.6) является двойственной по отношению к задаче (3.1)-(3.3) и, наоборот, если исходной является задача (3.4)-(3.6), то двойственной к ней будет модель (3.1)-(3.3). Такие задачи называются симметричными.

Таким образом, двойственную задачу можно получить по следующим правилам:

1) коэффициенты c_j (j=1,2, …, n) целевой функции (3.1) прямой задачи служат свободными членами основных ограничений (3.5) двойственной задачи, а свободные члены b₁, b₂, …,b_m основных ограничений (3.2) исходной задачи являются коэффициентами целевой функции (3.4) двойственной задачи.

Итак, число переменных у₁, у₂, …, у_m в двойственной задаче равно m – числу основных ограничений исходной задачи, а число основных ограничений двойственной задачи равно n – числу переменных исходной задачи;

2) матрица коэффициентов основных ограничений двойственной задачи является транспонированной по отношению к матрице А коэффициентов при переменных в основных ограничениях исходной задачи;

3) неравенства основных ограничений исходной задачи имеют знак «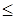», а неравенства двойственной задачи – «»;

4) целевая функция (3.1) исходной задачи – на максимум, а двойственной (3.4) – на минимум.

Если в исходной задаче ограничения выражены равенствами, то соответствующая ей двойственная задача будет иметь ограничения- неравенства. Такие задачи называются несимметричными:

Исходная задача	Двойственная задача
.
.	.

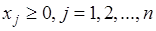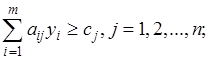
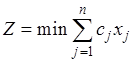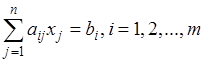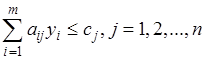Основные утверждения о взаимно двойственных задачах содержатся в следующих теоремах.

Первая теорема двойственности. Если одна задача из пары двойственных обладает оптимальным решением, то и другая имеет оптимальное решение, причем экстремальные значения соответствующих целевых функций равны

.

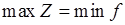Если же у одной из этих задач целевая функция не ограничена, то двойственная ей задача не имеет допустимых решений. Наконец, если одна из этих задач не имеет допустимых решений, то двойственная ей задача либо также не имеет допустимых решений, либо имеет неограниченную целевую функцию.

Вторая теорема двойственности. Для того, чтобы два допустимых решения и У =(у₁, у₂, …, у_m) пары двойственных задач были оптимальными необходимо и достаточно, чтобы они удовлетворяли так называемым «условиям дополняющей нежесткости»:

1)

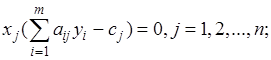
2)

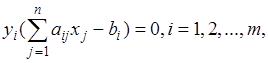
т.е. чтобы равнялось нулю произведение значений любой переменной одной задачи на разность между значениями левой и правой частей соответствующего ограничения двойственной задачи.

Третья теорема двойственности (теорема об оценках). Значения переменных у_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов ограничений исходной задачи на экстремальное значение ее целевой функции Z _max, т.е.

.

Дата добавления: 2014-11-18