Симметричный симплекс-метод

ПРОГРАММИРОВАНИЯ

СИМПЛЕКС-МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО

Контрольные вопросы к разделу 1

1. Каков экономический смысл целевой функции в задаче математического программирования?

2. В чем отличие оптимального плана от допустимого плана модели математического программирования?

3. Каким образом нахождение минимума целевой функции можно свести к решению задачи на ее максимум?

4. Чем задачи линейного программирования отличаются от задач нелинейного программирования?

5. Придумайте модель линейного и модель нелинейного программирования.

6. Пусть в ходе решения задачи линейного программирования определен многоугольник области допустимых решений. В какой части допустимой области целевая функция принимает экстремальное значение?

7. Как определить линию уровня целевой функции, соответствующую некоторой константе C?Каким образом относительно нее будут располагаться все другие линии уровня этой функции.

8. Как определить направления наискорейшего возрастания целевой функции?

Если в задаче линейного программирования больше двух неизвестных, то графический метод для ее решения не пригоден. В этом случае задачу решают симплекс-методом.

Симплекс-метод относится к классу итерационных численных методов: расчет начинают с определения некоторого начального приближения к решению (в симплекс-методе его называют опорным планом) и затем, посредством многократного применения определенной вычислительной процедуры получают результат (оптимальный план).

Рассмотрим применение симплекс-метода на примере решения конкретной задачи.

Задача 2.1.

Предприятие может производить три вида продукции: А, В, С. При этом используются два вида ресурсов. В таблице даны удельные расходы ресурсов и цены для каждого вида продукции. Общий объем выпуска всех видов продукции не должен превышать 6000 ед.

Таблица– Расход ресурсов на единицу выпуска продукции и цены

Ресурсы	Продукция	Объем ресурсов
А	В	С
Ресурс 1, ед.ресурса/ед. выпуска
Ресурс 2, ед.ресурса/ед. выпуска
Цена продукции, ден.ед.				-

Определить сколько продукции каждого вида должно производить предприятие, чтобы получить максимум валового продукта в денежном выражении.

РЕШЕНИЕ.

Обозначим неизвестные:

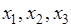– выпуски продукции видов А, В, С соответственно.

Целевая функция имеет смысл валового продукта в денежном выражении. Выразим его через неизвестные :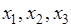

(2.1)

Запишем ограничения на ресурсы:

; (2.2)

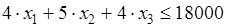. (2.3)

Ограничение на суммарный объем выпуска:

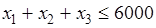. (2.4)

Алгоритм симплекс-метода следующий.

1 З а п и с ь з а д а ч и в к а н о н и ч е с к о й ф о р м е.

В канонической форме задача линейного программирования имеет ограничения в форме равенств. Преобразуем неравенства (2.2)-(2.4) в равенства путем введения в каждое ограничение дополнительной переменной. В целевую функцию (2.1) дополнительные переменные вводятся с коэффициентом «0».

+0·() (2.5)

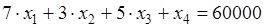; (2.6)

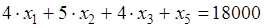; (2.7)

. (2.8)

.

В ограничениях (2.5)-(2.8) 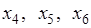являются дополнительными переменными.

2 В ы б о р о п о р н о г о п л а н а.

В качестве опорного плана примем нулевые значения основных переменных:

.

Подставив эти значения в выражение целевой функции (2.5) и ограничения (2.6)-(2.8), получим:

, , .

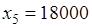3 С о с т а в л е н и е п е р в о н а ч а л ь н ой с и м п л е к с-т а бл и ц ы.

В базисный столбец таблицы 1 записывают дополнительные переменные, в столбец «В» – значения базисных переменных, в строки базисных переменных – коэффициенты из ограничений (2.6)-(2.8), в последнюю строку вносят значение целевой функции и ее коэффициенты с обратным знаком.

Таблица 1 – Первоначальная симплекс-таблица

Базис	В	х1	х2	х3	х4	х5	х6
х4 х5 х6
М+1		-9	-8	-10

3 О п р е д е л е н и е р а з р е ш а ю щ е й с т р о к и,

разрешающего столб а и разрешащ его элемента.

Разрешающий столбец выбирают по коэффициентам строки «М+1». При решении задач максимизации разрешающий столбец соответствует наибольшему по модулю отрицательному элементу (столбец х₃). Переменная х₃ будет введена в базис в следующем приближении к оптимальному плану (таблица 2). Чтобы определить: какая переменная будет вытеснена из базиса, находим разрешающую строку по минимуму отношений коэффициентов столбца «В» к соответствующим положительным элементам разрешающего столбца.

.

Таким образом, из базиса будет вытеснена переменная х₅. Разрешающий элемент находится на пересечении разрешающей строки и разрешающего столбца.

Если решается задача минимизации целевой функции, то разрешающий столбец следует выбирать по максимальному положительному элементу последней строки симплекс-таблицы (коэффициент, принадлежащие столбцу «В» не рассматривают).

4 Р а с ч е т о ч е р е д н о й с и м п л е к с – т а б л и ц ы.

Расчет следующей симплекс-таблицы начинают с разрешающей строки: ее элементы делят на разрешающий элемент; результат записывают в новую таблицу (подчеркнутая строка в таблице 2). Остальные строки таблицы вычисляют по правилу: из рассчитываемой строки почленно вычитается подчеркнутая строка, умноженная на элемент, принадлежащий одновременно рассчитываемой строке и разрешающему столбцу.

(60000 7 3 5 1 0 0) (60000 7 3 5 1 0 0)

х₄: – = – =

(4500 1 1,25 1 0 0,25 0)·5 (22500 5 6,25 5 0 1,25 0)

= (37500 2 -3,25 0 1 -1,25 0).

(6000 1 1 1 0 0 1)

х₆: – = (1500 0 -0,25 0 0 -0,25 1).

(4500 1 1,25 1 0 0,25 0)·1

(0 -9 -8 -10 0 0 0)

Z: – = (45000 1 -4,5 0 0 2.5 0).

(4500 1 1,25 1 0 0,25 0)·(-10)

Таблица 2 – Cимплекс-таблица

Базис	В	х1	х2	х3	х4	х5	х6
х4 х3 х6	4500	1	-3.25 1.25 -0.25	1	0	-1.25 0.25 -0.25	0
М+1			4.5			2.5

Выполнена первая итерация; получен новый план задачи линейного программирования.

5 П р о в е р к а к р и т е р и я о п т и м а л ь н о с т и.

При решении задачи максимизации план является оптимальным, если в последней строке симплекс-таблицы (строка «М+1») отсутствуют отрицательные элементы. При решении задачи минимизации критерием оптимальности плана является отсутствие положительных коэффициентов в строке «М+1»; это условие не относится к значению целевой функции, расположенном на пересечении строки «М+1» и столбца «В».

Так как в таблице 2 критерий оптимальности выполнен, итерационный процесс прекращается. В случае невыполнения критерия следует продолжить решение в соответствии с пунктами алгоритма 3-5.

6 З а п и с ь о п т и м а л ь н о г о п л а н а.

Оптимальные значения переменных и целевой функции расположены в столбце «В»; не вошедшие в базис переменные равны нулю.

Оптимальный план:

, , .

, , ,

.

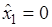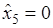Дата добавления: 2014-11-18