Метод Лагранжа

Классификация задач математического программирования

ПРОГРАММИРОВАНИЯ

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ НЕЛИНЕЙНОГО

Контрольные вопросы к разделу 4

Схема решения транспортной задачи

Перечислим основные этапы решения транспортной задачи.

1. Проверяют условие замкнутости. Если задача открытая, транспортную таблицу дополняют или столбцом фиктивного пункта потребления, или строкой фиктивного поставщика.

2. Строят опорный план.

3. Проверяют опорный план на невырожденность. Если для выполнения условия невырожденности не хватает занятой клетки, одну из клеток транспортной таблицы заполняют поставкой, равной нулю. При необходимости допустимо записывать нулевые поставки в несколько клеток.

4. План проверяют на оптимальность.

5. Если условия оптимальности не выполняются, переходят к следующему плану путем перераспределения поставок. Вычислительный процесс повторяется до получения оптимального плана.

1. Каков смысл целевой функции в математической модели транспортной задачи?

2.Каков смысл ограничений в математической модели транспортной задачи?

3. Можно ли применить метод потенциалов для решения открытой (незамкнутой) транспортной задачи?

4.Какие изменения необходимо внести в исходную транспортную таблицу, чтобы задачу можно было решить методом потенциалов?

5.В чем суть метода минимального элемента? Какой этап решения транспортной задачи будет выполнен в результате применения этого метода?

6. Как узнать является ли план перевозок оптимальным?

7. В каком случае и каким образом необходимо выполнить перераспределение поставок в плане перевозок?

8. Допустим построенный план перевозок является вырожденным. Можно ли продолжить решение задачи методом потенциалов и что для этого необходимо предпринять?

Общая задача математического программирования была сформулирована в разделе 1.1. В зависимости от типа функций, входящих в модель (1.1)-(1.3), задачу относят к тому или иному виду математического программирования. Различают линейное программирование (все функции линейны), целочисленное (решение представляют целые числа), квадратичное (целевая функция является квадратичной формой), нелинейное (хотя бы одна из функций задачи нелинейна) и стохастическое программирование (включены параметры, имеющие вероятностный характер).

Класс задач нелинейного программирования шире класса линейных моделей. Например, производственные затраты в большинстве случаев не пропорциональны объему выпуска, а зависят от него нелинейно, доход от реализации продуктов производства оказывается нелинейной функцией цен и т.д. Критериями в задачах оптимального планирования часто служат максимум прибыли, минимум себестоимости, минимум капитальных затрат. В качестве переменных величин выступают объемы выпуска различных видов продукции. В число ограничений входят производственные функции, характеризующие связь между выпуском продукции и затратами трудовых и материальных ресурсов, объем которых лимитирован.

В отличие от линейного программирования, в котором применяется универсальный метод решения (симплекс-метод), для решения нелинейных задач существует целый спектр методов в зависимости от формы входящих в модель функций. Из всего многообразия методов нами будут рассмотрены только два: метод Лагранжа и метод динамического программирования.

С уть метода Лагранжа заключается в сведении задачи на условный экстремум к решению задачи безусловного экстремума. Рассмотрим модель нелинейного программирования:

(5.1)

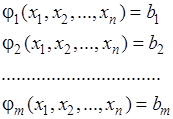(5.2)

где 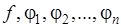– известные функции,

а 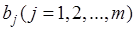– заданные коэффициенты.

Отметим, что в данной постановке задачи ограничения заданы равенствами, отсутствует условие неотрицательности переменных. Кроме того, полагаем, что функции 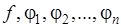непрерывны со своими первыми частными производными.

Преобразуем условия (5.2) таким образом, чтобы в левых или правых частях равенств стоял ноль:

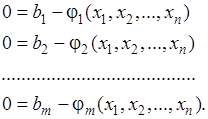(5.3)

Составим функцию Лагранжа. В нее входит целевая функция (5.1) и правые части ограничений (5.3), взятые соответственно с коэффициентами 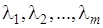. Коэффициентов Лагранжа будет столько, сколько ограничений в задаче.

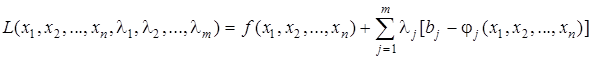
(5.4)

Точки экстремума функции (5.4) являются точками экстремума исходной задачи и наоборот: оптимальный план задачи (5.1)-(5.2) является точкой глобального экстремума функции Лагранжа.

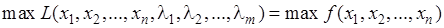. (5.5)

Действительно, пусть найдено решение 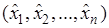задачи (5.1)-(5.2), тогда выполняются условия (5.3). Подставим план 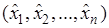в функцию (5.4) и убедимся в справедливости равенства (5.5).

Таким образом, чтобы найти оптимальный план исходной задачи, необходимо исследовать на экстремум функцию Лагранжа. Функция имеет экстремальные значения в точках, где ее частные производные равны нулю. Такие точки называются стационарными.

Определим частные производные функции (5.4)

,

.

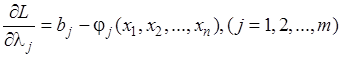После приравнивания нулю производных получим систему m+n уравнений с m+n неизвестными

, (5.6)

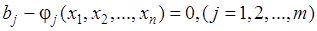. (5.7)

В общем случае система (5.6)-(5.7) будем иметь несколько решений, куда войдут все максимумы и минимумы функции Лагранжа. Для того чтобы выделить глобальный максимум или минимум, во всех найденных точках вычисляют значения целевой функции. Наибольшее из этих значений будет глобальным максимумом, а наименьшее – глобальным минимумом. В некоторых случаях оказывается возможным использование достаточных условий строгого экстремума непрерывных функций (см. ниже задачу 5.2):

пусть функция непрерывна и дважды дифференцируема в некоторой окрестности своей стационарной точки 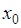(т.е. )). Тогда:

а) если , (5.8)

то 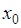– точка строгого максимума функции ;

б) если , (5.9)

то 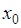– точка строгого минимума функции ;

г ) если ,

то вопрос о наличии экстремума остается открытым.

Кроме того, некоторые решения системы (5.6)-(5.7) могут быть отрицательными. Что не согласуется с экономическим смыслом переменных. В этом случае следует проанализировать возможность замены отрицательных значений нулевыми.

Экономический смысл множителей Лагранжа. Оптимальное значение множителя показывает на сколько изменится значение критерия Z при увеличении или уменьшении ресурса j на одну единицу, так как

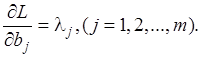
Метод Лагранжа можно применять и в том случае, когда ограничения представляют собой неравенства. Так, нахождение экстремума функции 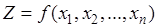при условиях

,

выполняют в несколько этапов:

1. Определяют стационарные точки целевой функции, для чего решают систему уравнений

.

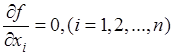2. Из стационарных точек отбирают те, координаты которых удовлетворяют условиям

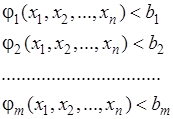
3. Методом Лагранжа решают задачу с ограничениями-равенствами (5.1)-(5.2).

4. Исследуют на глобальный максимум точки, найденные на втором и третьем этапах: сравнивают значения целевой функции в этих точках – наибольшее значение соответствует оптимальному плану.

Задача 5.1 Решим методом Лагранжа задачу 1.3, рассмотренную в первом разделе. Оптимальное распределение водных ресурсов описывается математической моделью

.

.

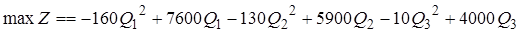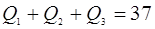Составим функцию Лагранжа

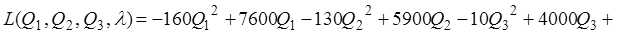
Найдем безусловный максимум этой функции. Для этого вычислим частные производные и приравняем их к нулю

,

Таким образом, получили систему линейных уравнений вида

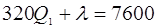
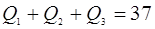
Решение системы уравнений представляет собой оптимальный план распределения водных ресурсов по орошаемым участкам

, .

Величины измеряются в сотнях тысяч кубических метров. - величина чистого дохода на одну сотню тысяч кубических метров поливной воды. Следовательно, предельная цена 1 м³ оросительной воды равна 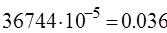ден. ед.

Максимальный дополнительный чистый доход от орошения составит

=

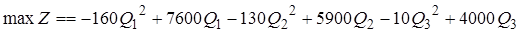-160·12,26²+7600·12,26-130·8,55²+5900·8,55-10·16,19²+4000·16,19=

= 172391,02 (ден. ед.)

Задача 5.2 Решить задачу нелинейного программирования

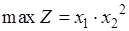
Ограничение представим в виде:

.

Составим функцию Лагранжа и определим ее частные производные

.

.

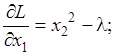
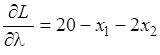Чтобы определить стационарные точки функции Лагранжа, следует приравнять нулю ее частные производные. В результате получим систему уравнений

.

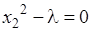
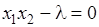
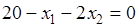Из первого уравнения следует

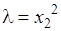. (5.10)

Выражение подставим во второе уравнение

,

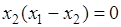откуда следует два решения для :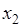

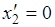и . (5.11)

Подставив эти решения в третье уравнение, получим

, .

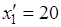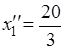Значения множителя Лагранжа и неизвестной 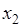вычислим по выражениям (5.10)-(5.11):

, , , .

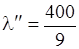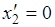Таким образом, получили две точки экстремума:

; .

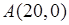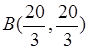Для того чтобы узнать являются ли данные точки точками максимума или минимум, воспользуемся достаточными условиями строгого экстремума (5.8)-(5.9). Предварительно выражение для 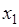, полученное из ограничения математической модели, подставим в целевую функцию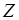

,

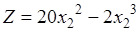. (5.12)

Для проверки условий строгого экстремума следует определить знак второй производной функции (5.11) в найденных нами экстремальных точках 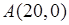и .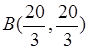

, ;

.

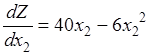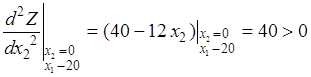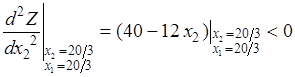Таким образом, (·) 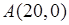является точкой минимума исходной задачи (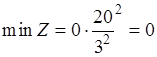), а (·) 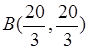– точкой максимума.

Оптимальный план:

, , ,

.

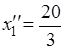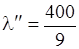Дата добавления: 2014-11-18