Математического программирования

НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ МОДЕЛИ

Контрольные вопросы к разделу 5

1. Каким условиям должна удовлетворять модель математического программирования, чтобы для ее решения можно было применить метод Лагранжа?

2. Допустим, модель нелинейного программирования имеет пять переменных и семь ограничений, сколько коэффициентов Лагранжа следует включить в функцию Лагранжа?

3. Какая связь существует между экстремумами целевой функции и функции Лагранжа?

4. Каков экономический смысл функции Лагранжа?

5. Можно ли применять метод Лагранжа для решения задач нелинейного программирования с ограничениями- неравенствами?

6. Каким условиям должна удовлетворять модель математического программирования, чтобы для ее решения можно было применить метод динамического программирования?

7. Допустим, задача нелинейного программирования имеет аддитивную целевую функцию, семь переменных и два ограничения. Сколько шагов будет в решении этой задачи методом динамического программирования?

8. Сколько неизвестных содержится в оптимизационной задаче, представляющей собой шаг динамического программирования?

Задача о смесях. Из имеющихся видов сырья нужно получить путем смешивания новый продукт с заданными характеристиками. Стоимость смеси должна быть минимальной.

Смесь состоит из n видов сырья, каждый из которых содержит m видов веществ.

Пусть 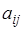– количество i-го вещества в единице j-го вида сырья, цена которого – .

и – соответственно наименьшее и наибольшее допустимое количество i-го вещества в смеси.

– объем j-го сырья.

Неизвестные – количество сырья j–го вида, которое будет использовано для производства смеси. Общая стоимость смеси должна быть минимальна.

Математическая модель:

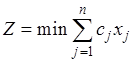
Задача об оптимальном плане выпуска продукции. Пусть для изготовления каждого из n видов продукции требуется m видов ресурсов.

Известны: 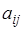– расход i-го ресурса на единицу j-го вида продукции ();

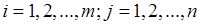– прибыль от реализации единицы j-й продукции;

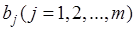– запасы ресурсов;

– нижний и, соответственно, верхний допустимый объем j-й продукции.

Требуется определить – объем выпуска каждого вида продукции. Причем прибыль от реализации всех видов продукции должна быть максимальной при имеющихся объемах ресурсов и ограничениях на выпуски каждого вида продукции.

Математическая модель:

.

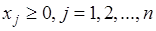Задача планирования производства с помощью производственной функции. Пусть выпуск продукции на предприятии описывает производственная функция

.

Здесь – выпуск предприятия;

a1, a2, …, an – известные числовые параметры, которые получаются с помощью статистической обработки исходных данных;

– факторы производства.

Обозначим 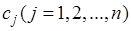– затраты, связанные с использованием единицы j -го фактора.

Требуется максимизировать выпуск продукции

при условиях:

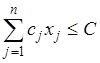(ограничение на суммарные затраты всех факторов);

.

Основная задача производственного планирования. Для выпуска комплектной продукции (например, агрегата механизмов) имеется 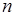технологий. В одном комплекте элементов -го вида 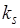штук (s= 1,2, …, l).

Для производства деталей комплекта используются m видов сырья, количество которых задано: 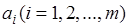. При этом за один производственный цикл по j -й технологии (j= 1,2, …, n) i -й ингредиент расходуется в количестве 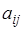единиц и деталей s -го вида получается штук.

Требуется определить план производства, представляющий собой интенсивности применения каждой технологии. Под интенсивностью применения некоторой j -й технологии понимают – число циклов производства по данной технологии. Задача заключается в выборе плана , максимизирующего число полных комплектов продукции, при заданных ограничениях на объемы используемых видов сырья.

По плану i -й ингредиент расходуется в количестве

единиц и деталей s -го вида получается штук, что позволяет их использовать для составления комплектов и, таким образом, число полных комплектов равно

.

Необходимо максимизировать число полных комплектов при ограничениях на использование имеющихся запасов ресурсов:

;

;

.

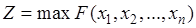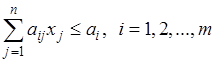Задача оптимизации межотраслевых потоков. Пусть каждая из отраслей народного хозяйства производит только один продукт . Эта продукция используется другими отраслями в качестве сырья, а также расходуется на удовлетворение конечного спроса (потребление, инвестиции, экспорт).

Известны:

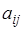() – удельные расходы каждого вида продукции на производство всех других видов;

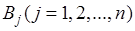– максимально возможный объем производства каждого продукта и его минимальный объем 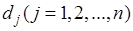для внепроизводственного потребления;

– стоимость единицы продукции j -го вида.

В задаче требуется найти такой план производства и такой план конечной продукции , чтобы общая стоимость конечной продукции была максимальной при ограничениях на объемы производства, выпуск конечной продукции и технологических ограничениях на выпуск продукции.

;

ограничения на объемы производства: , ;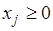

ограничения на выпуск конечного продукта: ;

технологические ограничения на выпуск продукции

.

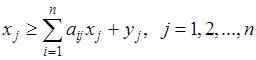Задача о назначениях. Имеется n механизмов (работников), которые нужно распределить по n работам так, чтобы при заданной производительности каждого механизма (работника) на каждой из работ, суммарный эффект был максимальным.

Пусть () – производительность i -го механизма (работника) на j -й работе;

Требуется отыскать такой план 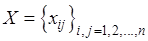распределения механизмов по вида работ, при котором суммарная производительность всех механизмов максимальна, т.е.

при ограничениях:

1) каждый механизм выполняет одну работу

;

2) каждый вид работы выполняется только одним механизмом

Кроме описанных выше, к часто используемым математическим моделям относятся:

– задача оптимизации раскроя материалов;

– задача оптимальной загрузки оборудования;

– задача размещения и развития производства;

– задача оптимизации отраслевой структуры агрофирмы.

СОДЕРЖАНИЕ

…………………………………………………………………………………с.

Введение

1 Общая задача математического программирования

1.1 Модель математического программирования……………………..

1.2 Математическая формулировка задач линейного

программирования ……………………………………………………

1.3 Примеры построения простейших моделей математического

программирования………………………………………………………

1.4 Геометрическая интерпретация задач линейного

программирования, графический метод решения ………………………

1.4.1 Графический метод решения ……………………………………

1.4.2 Схема решения задачи графическим методом ………………….

1.4.3 Особые случаи решения задач линейного программирования..

1.5 Контрольные вопросы к разделу 1

2 Симплекс-метод решения задач линейного программирования………

2.1 Симметричный симплекс-метод…………………………………

2.2 Экономический анализ оптимального плана по последней

симплекс-таблице………………………………………………………….

2.3 Симплекс-метод с искусственным базисом…………………………

2.4. Схема решения задач линейного программирования

симплекс-методом ………………………………………………………..

2.5. Особые случаи при решении задач симплекс-методом…………….

2.6 Контрольные вопросы к разделу 2 …………………………………..

3 Двойственные задачи линейного программирования ………………….

3.1 Понятие о двойственных задачах …………………………………..

3.2 Теоремы двойственности в линейном программировании ………..

3.3 Экономическая интерпретация двойственных задач ……………

3.4. Примеры построения двойственных задач ………………………..

3.5 Контрольные вопросы к разделу 3 ………………………………….

4 Транспортная задача линейного программирования ……………………

4.1 Математическая постановка транспортной задачи ……………….

4.2 Метод потенциалов решения транспортной задачи ……………….

4.3 Схема решения транспортной задачи методом потенциалов ……

4.4 Контрольные вопросы к разделу 4 …………………………………

5 Методы решения задач нелинейного программирования ……………….

5.1 Классификация задач математического программирования ………

5.2 Метод Лагранжа ………………………………………………………

5.3 Метод динамического программирования ………………………….

5.4 Применение динамического программирования для решения задач о замене оборудования и эффективного использования ресурсов ……

5.5 Контрольные вопросы к разделу 5 ………………………………..

6 Наиболее распространенные модели математического

программирования ……………………………………………………..

ЛИТЕРАТУРА

1 Компьютерные технологии вычислений в математическом моделировании: Учеб. пособие для студ. вузов, обуч. по экон. спец. – М.: Финансы и статистика, 2001. – 255 с.

2 Шапкин А.С., Мазаева Н.П. Математические методы и модели исследования операций: Учебник. – М.: Издательско-торговая корпорация «Дашков и К», 2003. – 400 с.

3 Волков С.Н. Экономико-математические методы и модели: Учебник для студентов вузов. – М.: Колос, 2001. – 696 с. 40 экз.

4 Бережная В.В., Бережной В.И. Математические методы моделирования экономических систем: Учеб. Пособие для вузов по спец. «Финансы и кредит», «Бухучет, анализ и аудит», «Мировая экономика» - М.:Финансы и статистика, 2001. – 367 с. 1 экз.

5 Филькин Г.В., Захарченко Н.С. Моделирование социально-экономических систам: методические указания к практическим занятиям для студентов специальности 060900. – Новочеркасск, 2002. – 21 с.

6 Иванов П.В., Абраменко П.И. Математическое программирование: методические указания по выполнению контрольной работы (для студ. заоч. спец. 061100 – «Менеджмент организации», 030500 – «Профессиональное обучение») – Новочеркасск, 2002. – 26 с.

Учебное издание

Захарченко Наталья Степановна

Дата добавления: 2014-11-18