
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ресурсов
|
|
|
|
Применение динамического программирования для решения задач о замене оборудования и эффективного использования
Задача эффективного использования ресурсов. Имеется некоторое количество ресурса 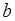 , которое можно использовать различными способами. Пусть
, которое можно использовать различными способами. Пусть 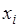 – количество ресурса, используемое
– количество ресурса, используемое 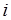 -м способом,
-м способом, 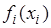 – доход от использования ресурса
– доход от использования ресурса 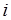 -м способом (
-м способом (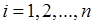 ).
).
Требуется распределить общее количество ресурса 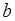 между различными способами, чтобы суммарный доход был максимальным.
между различными способами, чтобы суммарный доход был максимальным.
Модель оптимального использования ресурса имеет вид:
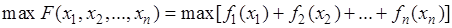 (5.13)
(5.13)
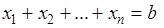 (5.14)
(5.14)

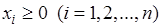 . (5.15)
. (5.15)
Вместо одной оптимизационной задачи (5.13)-(5.15), с заданным количеством ресурса и содержащей 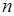 неизвестных, в методе динамического программирования решается
неизвестных, в методе динамического программирования решается 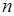 задач, в каждой из которых максимум находится лишь по одной переменной. Таким образом, процесс поиска решения исходной задачи как бы разворачивается во времени по шагам.
задач, в каждой из которых максимум находится лишь по одной переменной. Таким образом, процесс поиска решения исходной задачи как бы разворачивается во времени по шагам.
На последнем шаге определяется функция
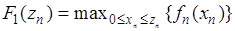 .
.
Для всех остальных шагов используется рекуррентное соотношение
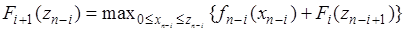 ,
, 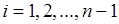 ,
,
здесь 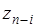 – количество ресурса, оставшееся для распределения к началу
– количество ресурса, оставшееся для распределения к началу 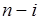 -го шага.
-го шага.
Очевидно,
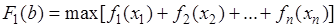 .
.
Метод динамического программирования можно использовать и в случае распределения нескольких видов ресурсов, однако, с увеличением размерности решение становится все более сложным.
Задача 5.3 Необходимо составить план вложений денежных средств в три отделения предприятия, исходя из общей суммы средств, которая равна 250 денежным единицам.
Известны функции прибыли fi(xi) по каждому отделению, где x i - средства, вкладываемые в i-е отделение (таблица 5.1). Размеры вложений ограничены: для первого отделения суммой 250 ден. ед., для второго отделения – 100 ден. ед.; для третьего - 250 ден. ед.
Найти оптимальное распределение денежных средств по отделениям, соответствующее максимуму суммарной но трем отделениям прибыли.
Таблица 5.1– Функции прибыли по трем отделениям
| xi | ||||||
| fi | ||||||
| f1 | ||||||
| f2 | - | - | - | |||
| f3 |
решение.
Введем обозначения:
x1 - количество вложенных денежных средств в первое отделение;
x2 - количество вложенных денежных средств во второе отделение;
x3 - количество вложенных денежных средств в третье отделение.
Целевая функция имеет смысл суммарной но трем отделениям прибыли.
Математическая модель задачи
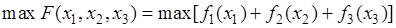
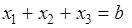

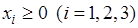 .
.
Процесс решения начинаем с последнего шага, т.е. оптимизируем вложение денежных средств в третье отделение. При этом мы не знаем: сколько осталось денег после вложения в первые два отделения. Обозначим величину оставшихся для вложения денег 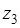 . Таким образом, переменная
. Таким образом, переменная 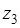 выражает всевозможные варианты условий начала последнего шага. Уравнение Беллмана для последнего шага имеет вид:
выражает всевозможные варианты условий начала последнего шага. Уравнение Беллмана для последнего шага имеет вид:
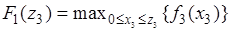 ,
,
x3 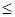 250.
250.
Поскольку функции прибыли fi(xi) заданы таблично, метод динамического программирования будем применять в табличном виде.
Так как с ростом x3 функция f3(x3) возрастает, то на последнем этапе все оставшиеся средства нужно отдать третьему отделению, таким образом,  x3 = z3.
x3 = z3.
Таблица 5 .2 – Условно-оптимальные планы для третьего отделения
| z3 | ||||||
| x3 | ||||||
| F1(z3 ) |
Запишем уравнение Беллмана для второго шага распределения средств:
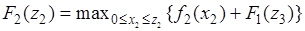 (5.16)
(5.16)
x2 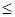 100
100  ,
,
здесь 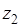 – средства, оставшиеся для вложений во второе и третье отделение, следовательно,
– средства, оставшиеся для вложений во второе и третье отделение, следовательно,
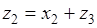 . (5.17)
. (5.17)
В таблицу 5.3 внесем все элементы формулы (5.16). В графы 2 и 4 записываем все возможные сочетания значений 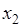 и
и 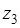 , которые в сумме составят величину
, которые в сумме составят величину 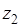 согласно выражению (5.17). При этом учитываем, что
согласно выражению (5.17). При этом учитываем, что
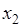 не должен превышать 100.
не должен превышать 100.
Таблица 5.3 – Условно-оптимальные планы для второго отделения
| z2 | x2 | f2(x2) | z3 | F1(z3 ) | f2(x2)+F1(z3) | F2(z2) |
Уравнение Беллмана для первого шага:
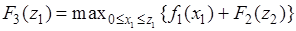 .
.
Переменная 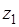 имеет смысл денежных средств для вложений во все три отделения предприятия и, следовательно, имеет единственное значение, равное общей сумме вложений 250 ден. ед. Значения функции F2(z2 ) будем брать из последнего столбца таблицы 5.3.
имеет смысл денежных средств для вложений во все три отделения предприятия и, следовательно, имеет единственное значение, равное общей сумме вложений 250 ден. ед. Значения функции F2(z2 ) будем брать из последнего столбца таблицы 5.3.
Таблица 5.4 – Условно-оптимальные планы для первого отделения.
| z1 | x1 | f1(x1) | z2 | F2(z2 ) | f1(x1)+F1(z3) | F1(z1) |
Мы выполнили шаги динамического программирования конца к началу. В результате чего определили максимальную суммарную прибыль от вложений во все отделения предприятия
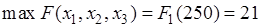 .
.
Теперь в ходе движения от первого шага к концу определим оптимальные величины вложений. Из таблицы 5.4 видим, что максимальная прибыль достигается при x1, равном 50, и z2, равном 200. Рассмотрим второй шаг (таблица 5.3). При z2, равном 200, функция Беллмана F2(z2) = 14. Это значение соответствует строке, в которой x2 равно 50, следовательно, на долю третьего отделения остается 150 денежных единиц.
Таким образом, максимум прибыли от вложения денежных средств составляет
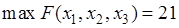 .
.
Оптимальный план вложений:
– в первое отделение 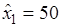 ден. ед.;
ден. ед.;
– во второе отделение 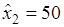 ден. ед.;
ден. ед.;
– в третье отделение 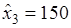 ден. ед..
ден. ед..
Задача о замене оборудования.
Задача 5.4 К началу пятилетнего периода на предприятии установлено новое оборудование. Зависимость производительности этого оборудования от времени его использования предприятием, а также зависимость затрат на содержание и ремонт оборудования при различном времени его использования приведены в таблице 5.5.
Таблица 5.5– Зависимость выпуска и эксплуатационных затрат от времени использования оборудования
| Показатель | Время 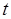 , в течение которого используется оборудование, год , в течение которого используется оборудование, год
| |||||
Выпуск продукции 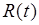 в стоимостном выражении, ден. ед. в стоимостном выражении, ден. ед.
| ||||||
Эксплуатационные затраты оборудования 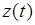 , ден. ед. , ден. ед.
|
Зная, что затраты, связанные с приобретением и установкой нового оборудования, идентичного с установленным, составляют 35 ден. ед., а заменяемое оборудование списывается, составить такой план замены оборудования в течение пятилетки, при котором общая прибыль за данный период максимальна.
решение.
Обозначим:
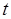 – время службы оборудования;
– время службы оборудования;
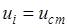 – принятие решения в начале
– принятие решения в начале 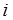 -го года об использовании имеющегося оборудования;
-го года об использовании имеющегося оборудования;
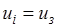 – принятие решения в начале
– принятие решения в начале 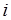 -го года о замене оборудования;
-го года о замене оборудования;
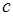 – стоимость нового оборудования.
– стоимость нового оборудования.
Целевая функция 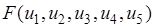 имеет смысл суммарной за пятилетний период прибыли.
имеет смысл суммарной за пятилетний период прибыли.
Математическая модель задачи
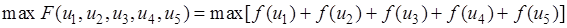 , (5.18)
, (5.18)
где 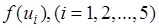 – прибыль предприятия за
– прибыль предприятия за 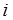 -й год.
-й год.
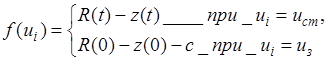 ,
,
Модель (5.18) относится к классу нелинейного программирования c булевыми (логическими) переменными. Целевая функция аддитивна. Поскольку задача имеет пять неизвестных, динамическое программирование также будет иметь пять шагов.
Уравнения Беллмана для последнегошага имеет вид:
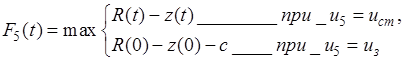 , (5.19)
, (5.19)
здесь 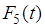 – функция максимальной прибыли за последний год в зависимости от возраста оборудования в начале года
– функция максимальной прибыли за последний год в зависимости от возраста оборудования в начале года 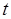 .
.
Уравнения Беллмана для 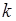 -го шага
-го шага
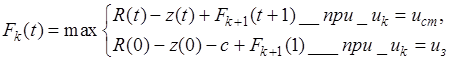 ;
; 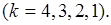 (5.20)
(5.20)
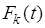 – максимальная прибыль, начиная с
– максимальная прибыль, начиная с 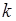 -го года и до конца периода в зависимости от возраста оборудования в начале
-го года и до конца периода в зависимости от возраста оборудования в начале 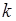 -го года.
-го года.
Планируем замену оборудования в начале пятого года. Предполагаем варианты условий начала данного шага, т.е. последовательно перебираем возможные значения возраста оборудования к началу пятого года. Расчеты проводим по уравнению (5.19). 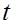 принимает значения: 1, 2, 3, 4. В результате получаем функцию максимальной прибыли за последний год в зависимости от возраста оборудования:
принимает значения: 1, 2, 3, 4. В результате получаем функцию максимальной прибыли за последний год в зависимости от возраста оборудования:
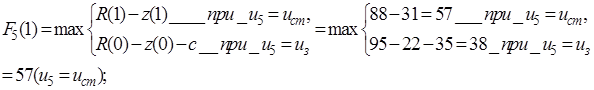
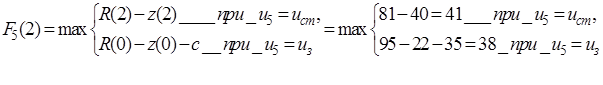
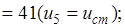 (5.21)
(5.21)
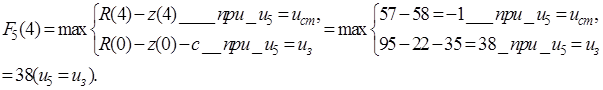
Планируем начало четвертого года. Расчеты проводим по уравнению (5.20). 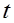 принимает значения: 1, 2, 3. Получаем функцию максимальной прибыли за последние два года в зависимости от возраста оборудования:
принимает значения: 1, 2, 3. Получаем функцию максимальной прибыли за последние два года в зависимости от возраста оборудования:
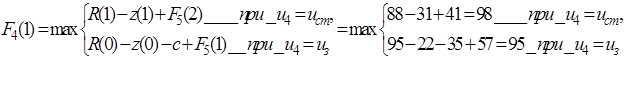
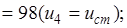 (5.22)
(5.22)
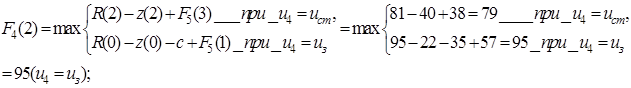
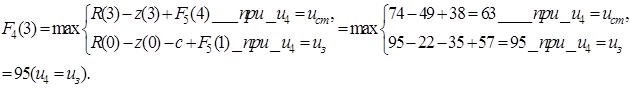
Планируем начало третьего года. Расчеты проводим по уравнению (5.20).  принимает значения: 1, 2. Получаем функцию максимальной прибыли за последние три года в зависимости от возраста оборудования:
принимает значения: 1, 2. Получаем функцию максимальной прибыли за последние три года в зависимости от возраста оборудования:
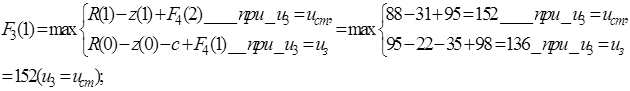
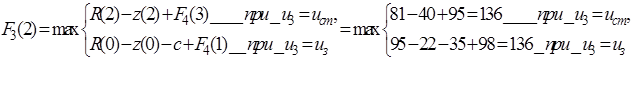
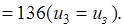 (5.23)
(5.23)
Планируем начало второго года. Расчеты проводим по уравнению (5.20). Получаем функцию максимальной прибыли за период со второго по пятый год:
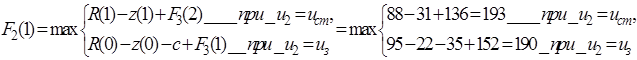
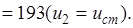 (5.24)
(5.24)
Планируем начало первого года.
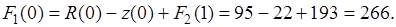 (5.25)
(5.25)
Значение функции Беллмана 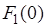 представляет собой максимальную прибыль предприятия за пятилетний период.
представляет собой максимальную прибыль предприятия за пятилетний период.
Мы выполнили расчет шагов динамического программирования от конца к началу периода. В результате определили
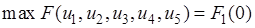 .
.
Теперь в направлении от начала периода до его конца найдем оптимальный план замены оборудования.
По условию задачи в начале первого года оборудование было обновлено, т.е. 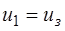 .
.
В выражение (5.25) входит значение 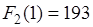 . Оно было вычислено по формуле (5.24) и соответствует
. Оно было вычислено по формуле (5.24) и соответствует 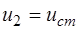 .
.
В свою очередь это выражение содержит значение 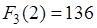 , вычисленное по (5.23) при
, вычисленное по (5.23) при 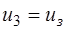 .
.
В (5.23) входит 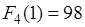 , вычисленное по (5.22) при
, вычисленное по (5.22) при 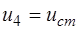 .
.
И, наконец, из выражения (5.21) ясно, что 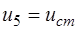 .
.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 427; Нарушение авторских прав?; Мы поможем в написании вашей работы!