Решение. Пример 2.Найти для функции f(x,y) = xy приращение и соответствующий полный дифференциал если x0 = 4

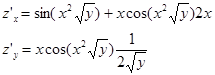
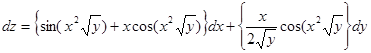
Пример 2. Найти для функции f (x, y) = xy приращение и соответствующий полный дифференциал если x ₀ = 4, y ₀ = 3, а x ₁ = 4,2 и y ₁ = 3,1.

Решение. Δ х = x ₁ - x ₀ = 0.2; Δ y = y ₁ - y ₀ =0.1.

D f (х, у) = f (х ₁, у ₁) - f (х ₀, у ₀) = x ₁ y ₁ + x ₀ y ₀ = 4.2 ּ 3.1 - 12 = 1.02

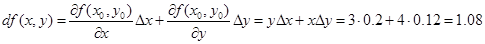
Следовательно, разность (рассогласование) между D f и d f составит 0.06.

Вторым дифференциалом функции двух переменых d² z называется диференциал от первого дифференциала

Опуская скобки и учитывая равенство смешанных производных получим

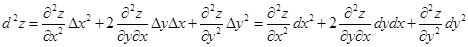(3.7)

Глава 4. Градиент и производная по направлению.

Пусть в каждой точке области D задана дифференцируемая функция двух переменных z = f (x, у). градиентом функции grad z в точке М(х, у) называется вектор, проекциями которого являются частные производные

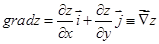. (4.1)

Аналогично определяется градиент функции трех переменных

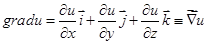(4.2)

Направление вектора градиента указывает направление наискорейшего изменения функции.

Длина вектор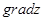а равна

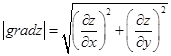(4.4)

Фналогично определяется и длина вектора .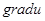

Для функции двух переменных в каждой точке М(х, у) вектор градиента перпендикулярен линии уровня.

Если задан вектор 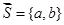. Производной функции по направлению вектора 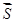называется проекция вектора градиента на направление вектора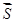

. (4.5)

Т.е. проекция равна скалярному произведению векторов 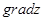и 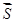делить на длину вектора .

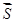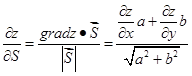(4.6)

Аналогично определяется производная по направлению вектора 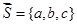и для функции трех переменных

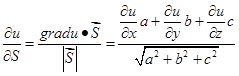(4.7)

Пример. Вычислить градиент функции 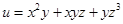в точке М(1,2,4) и производную по направлению .

Решение. Вычислим частные производные и найдем градиент функции

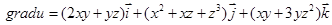(4.8)

Если в выражение (4.8) подставить координаты точки М, то получим градиент функции в точке М

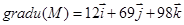
Вычислим производную по направлению вектора

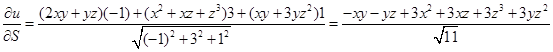
В точке М

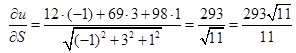
Глава 5. Экстремум функции двух переменных

Формула Тейлора для функции двух переменных

Формула Тейлора для функции одной переменной приведена в разделе 4

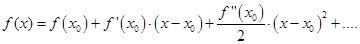
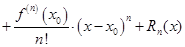
где 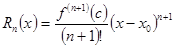остаточный член формулы Тейлора.он определяет погрешность, возникающую при замене функции на полином степени n.

Преобразуем формулу, обозначив за 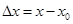и перенесем 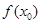налево. Тогда

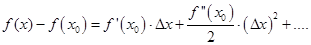
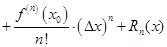
Разность 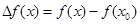есть приращение функции, а 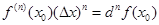. С учетом этих значений, получим дифференциальную форму формулы Тейлора

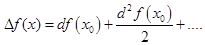
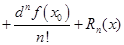(5.1)

Дифференциальная форма справедлива для функции любого числа переменных, в частности, для функции двух переменных,

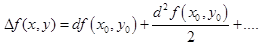
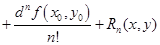(5.2)

Здесь

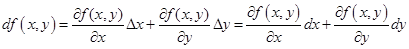
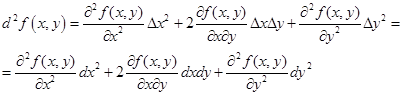
Максимум и минимум функции двух переменных.

Мы говорим, что функция двух переменных z = f (x, у) имеет максимум в точке М₀(x ₀, y ₀), если значение функции в этой точке больше чем во всех соседних точках

f (x ₀, у ₀) > f (x, у)

Аналогично, в точке минимума М₀(x ₀, y ₀) значение функции меньше чем во всех соседних точках

f (x ₀, у ₀) < f (x, у)

минимум и максимум функции достигаются только внутри области D.

Минимумы и максимумы называются экстремумами функции (рис. 3.1).

В точке максимума приращение функции отрицательно для любых соседних точек

Δ f (x, y) < 0 (5.3)

В точке минимума приращение всегда строго положительно

Δ f (x, y) > 0 (5.4)

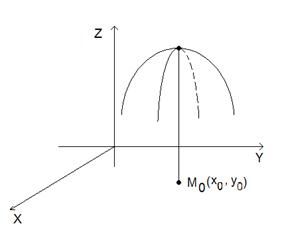
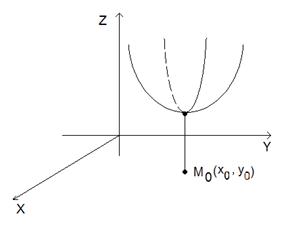
а б

Рис. 3.1. Максимум (а) и минимум (б) функции двух переменных.

Необходимые условия экстремума. В точке экстремума М₀(x ₀, y ₀) каждая частная производная первого порядка или равна нулю или не существует. Действительно, если мы зафиксируем у = y ₀, то функция f(x, у ₀) будет функцией одной переменной х, а для функции одной переменной в точке экстремума первая производная 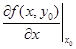или равна нулю или не существует. Аналогично, если х = x ₀, то равна нулю или не существует .

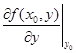Точки, в которых обе частные производные равны нулю называются стационарными точками. Для нахождения стационарной точки необходимо решить систему

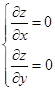(5.5)

Не все стационарные точку будут точками экстремума. Условие (5.5) является только необходимым условием, но не является достаточным.

Достаточные условия экстремума.

Теорема. Если в окрестности стационарной точки М₀(x ₀, y ₀) функция z = f (x, у) имеет непрерывные частные производные до третьего порядка включительно, то функция двух переменных имеет экстремум, если

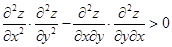(5.6)

При этом

если 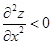, то достигается максимум (5.7)

если 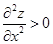, то достигается минимум. (5.8)

Если 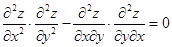, то требуется дальнейшее исследование.

Доказательство. Докажем для максимума, для минимума доказательство аналогично.

В стационарной точке обе частные производные равны нулю, следовательно равен нулю первый дифференциал 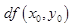и формула Тейлора начинается со второго слагаемого

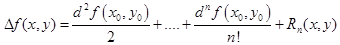
В точке максимума приращение Δ f (x, y) строго отрицательно Δ f (x, y) < 0. Следовательно, необходимо определить, при каких значениях вторых производных второй дифференциал сохраняет знак.

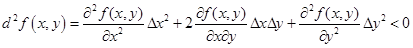
Вынесем за скобки положительную величину 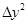=(Δу)², а отношение 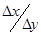обозначим за t 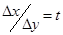. Получим квадратный трехчлен по переменной t, который сохраняет знак при любом значении t только если его дискриминант отрицателен

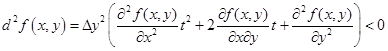
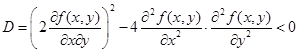
Или, сократив на 4 и переставив члены неравенства, получим

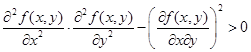
Знак квадратного трехчлена совпадает со знаком коэффициента при t ². Поэтому в точке максимума 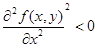. Теорема доказана.

Пример. Исследовать на экстремум функцию .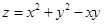

Решение. вычислим первые производные и найдем стационарную точку

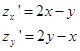
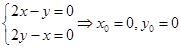
Вычислим вторые производные

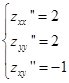
В стационарной точке

z_xx’’∙z_yy’’-(z_xy)²=2∙2-(-1)² > 0,

следовательно это точка экстремума.

Так как z_xx’’ > 0,то это точка минимума.

Глава 6. Метод наименьших квадратов.

Пусть функция 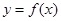задана таблично. Чаще всего это бывает при проведении экспериментальных исследований, когда значения функции непосредственно измеряются или вычисляются при проведении эксперимента.

В этом случае результаты записываются в таблицу, где первая строчка – значения независимой переменной х, а вторая – значения измеряемой переменной у.

Х	x1	x2	…………………..	xn
Y	y1	y2	…………………………….	yn

Требуется найти аналитическое выражение 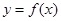, наилучшим образом описывающее имеющиеся экспериментальные данные.

На практике общий вид аналитического выражения обычно известен, а необходимо найти только неизвестные коэфициенты.

Проще всего эта задача решается для случая линейной зависимости, т.е. в том случае, когда есть основания считать, что

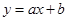(6.1)

Во многих случаях линейное приближение является достаточным. Эффективно это означает следующее: в формуле Тейлора отброшены все члены, кроме первых двух слагаемых

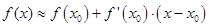(6.2)

Найдем неизвестные коэффициенты в выражении (6.1) методом наименьших квадратов.

Суть метода состоит в следующем: искомая прямая должна проходить так, чтобы было минимальным суммарное отклонение прямой от экспериментальных точек. Для этого вводится функция двух переменных S(a,b), задающая сумму квадратов отклонений экспериментальных точек от точек, лежащих на прямой. На рис. 5 экспериментальные значения обозначены черным, красным – прямая линия, коэффициенты a, b которой мы должны найти, отклонения показаны черными линиями. Минимизировать надо именно квадраты отклонений, так как сами отклонения имеют разные знаки и сумма их равна нулю.

Тем самым, подставив в (6.10) известные значения 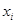из таблицы, мы вычислим соответствующие координаты 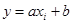точек, лежащих на прямой (красные точки на рис. 6) и вычисляем квадраты разности между 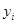и .

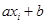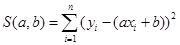(6.2)

Функция достигает минимума, если ее частные производные по a и b равны нулю. Вычислим производные и приравняем их нулю

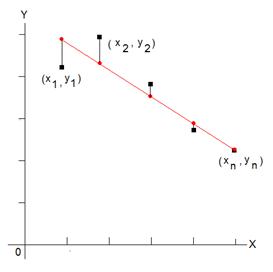
Рис. 5. Метод наименьших квадратов.

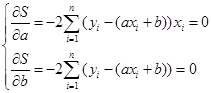
Или, раскрывая скобки, получим систему двух уравнений для нахождения чисел a и b

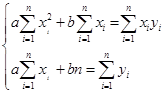
Аналогично можно искать аппроксимирующую функцию вида

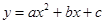
Пример. Даны экспериментально полученые пять значений искомой функции при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию в виде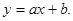

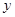
	4,2	5,0	3.9	2,7	2,4

Метод наименьших квадратов позволяет найти коэффициенты а и b линейной функции 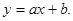Для этого составляется функция S(a, b)

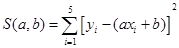
и определяется, при каких значениях коэффициентов достигается минимум функции S. Минимум достигается в стационарной точке, в которой обе частные производные обращаются в ноль.

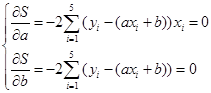
или

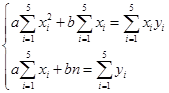
Составим расчетную таблицутаблицу

№	xi	yi	xi^2	xi· yi	у= f (xi)
		4,2		4,2	4,9
		5,0		10,0	4,3
		3,9		11,7	3,7
		2,7		10,8	3,0
		2,4		12,0	2,4
сумма		18,3		48,7

Подставим полученные выражения в систему

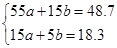а = - 0,62 b = 5,52

Искомое уравнение y = - 0,62 x + 5.52

Подставим в это уравнение х_i из таблицы, полученные значения занесены в последний столбец таблицы.

Глава 7. Числовые ряды.

Основные определения теории числовых рядов. Пусть задана бесконечная числовая последовательность

u₁, u₂, u₃,..., u_n... (7.1)

Числовым рядом называется бесконечная последовательность чисел, соединенная знаком плюс т.е. выражение

u₁ + u₂ + u₃ +... + u_n +... = 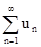. (7.2)

числа u₁, u₂, u₃,..., u_n,... называются членами ряда и являются элементами заданной последовательности (7.1).

Например, числовой ряд

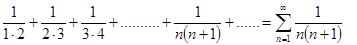(7.3)

имеет общий член u_n =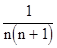

Сходимость и сумма ряда. Частичной суммой S_n называется сумма первых n членов ряда, т.е. S = u₁ + u₂ + u₃ ...+ u_n.

Частичные суммы ряда образуют новую последовательность - последовательность частичных сумм: S₁, S₂, S₃,..., S_n,.... Если существует конечный предел последовательности частичных сумм 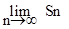= S < ¥, то ряд (7.2) называется сходящимся, а число S - суммой ряда. В этом случае пишут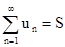

Если предел последовательности частичных сумм бесконечен или не существует, то ряд (7.2) называется расходящимся.

Пример. Определить сходимость ряда

Решение. Вначале запишем частичную сумму заданного ряда

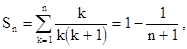
Рассмотрим предел частичных сумм

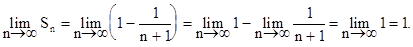
Следовательно, ряд (7.3) сходится и его сумма равна 1.

Пример. Дан числовой ряд

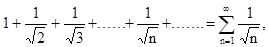
исследовать сходимость ряда.

Решение.

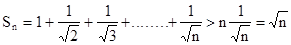
Величина 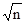бесконечно возрастает с ростом n. Поэтому предел последовательности S_n при n ® ¥ равен бесконечности и ряд расходится.

Пример. Определить сходимость следующего ряда:

1 - 1 + 1 - 1 + (-1)ⁿ⁺¹ +....

Решение. Четная частичная сумма этого ряда S_2n = 0, а нечетная - S_2n+1 = 1. Это означает, что предел 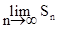не существует. Следовательно, данный ряд расходится.

Необходимое условие сходимости ряда. Для сходящихся числовых рядов всегда выполняется одно условие - его общий член стремится к нулю. Дадим строгую формулировку необходимого условия сходимости ряда.

Теорема о необходимом условии сходимости числового ряда. Если числовой ряд сходится, то его общий член при n ® ¥ стремится к нулю, т.е.

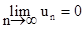(7.4)

Доказательство. Рассмотрим две соседние частичные суммы ряда (7.2)

S_n-1 = u₁ + u₂ + u₃ +... u_n-1,

S_n = u₁ + u₂ + u₃ +... u_n-1 + u_n.

Из сходимости ряда следует, что

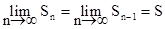
С другой стороны,

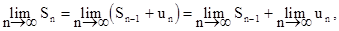
т.е.

S = S +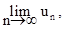

откуда и следует (7.4).

Введенное условие сходимости является лишь необходимым, но не достаточным. Это означает, что существуют расходящиеся ряды, у которых .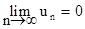

Пример. Покажем, что ряд

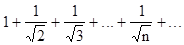
удовлетворяет необходимому условию сходимости ряда, но является расходящимся.

Действительно, необходимое условие выполняется, так как

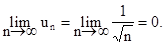
Чтобы доказать расходимость ряда, рассмотрим его n-ю частичную сумму:

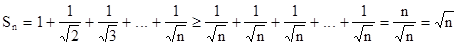
Очевидно, что ряд расходится, поскольку

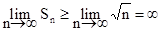
Основные свойства сходящихся числовых рядов.

Свойство 1. Добавление или отбрасывание конечного числа членов не изменяет сходимости ряда.

Доказательство. Пусть A - сумма отброшенных (добавленных) членов ряда, а S_n - частичная сумма исходного ряда (4.34). Тогда частичная сумма ряда с отброшенными (добавленными) членами имеет вид S^* = S_n ± A.

Поскольку A - конечное число, то

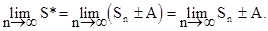
Следовательно, если существует то существует и

Свойство 2. Если ряд

u₁ + u₂ + u₃ +.... + u_n +... (7.5)

сходится и имеет сумму S, то ряд cu₁ + cu₂ +... + cu_n +.., получаемый из предыдущего умножением всех членов на одно и то же число с, также сходится и имеет сумму сּS.

Доказательство. Рассмотрим частичную сумму ряда (7.5):

s_n = cu₁ + cu₂ + cu₃ +... + cu_n = cּS_n.

Поэтому

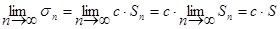
Свойство 3. Сходящиеся ряды можно почленно складывать и вычитать.

Доказательство. Пусть

u₁ + u₂ + u₃ +... + u_n +... = S;

v₁ + v₂ + v₃ +... + v_n +... = Ф,

тогда ряд

(u₁ ± v₁) + (u₂ ± v₂) +... + (u_n ± v_n) +...

также сходится и имеет сумму S ± Ф, так как

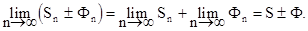
Дата добавления: 2014-11-18