Знакочередующиеся ряды

Знакочередующимися рядами называются ряды вида

u₁ - u₂ + u₃ - u₄ +......, (7.19)

где все u_n > 0.

Сходимость таких рядов исследуется по теореме Лейбница: если в знакочередующемся ряде u₁ - u₂ + u₃ - u₄ +......, u_n > 0 все члены таковы, что u₁ > u₂ > u₃ >u₄ .... и 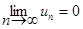, то ряд (4.51) сходится, его сумма положительна и не превосходит первого члена ряда u₁.

Доказательство. Возьмем сумму четного числа первых членов S _2m, которая положительна.

S_2m = (u₁ - u₂ ) + (u₃ - u₄ ) +......+ (u_2m-1 – u_2m) > 0,

так как выражение в каждой скобке больше нуля.

S_2m возрастает при росте m, т.к. S_2m = S_2(m-1) + (u_2m-1 – u_2m) > S_2(m-1).

С другой стороны

S_2m = u₁ - (u₂ - u₃ ) - (u₄ – u₅)......- (u_2m-2 - u_2m-1) – u_2m < u₁.

т. е. при росте m S_2m возрастает и ограничена сверху. Следовательно, имеет предел S= = .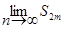

Нечетные суммы будут иметь тот же предел S_2m+1 = S_2m + u_2m+1

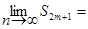
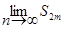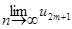+ = S + 0 = S.

.

Четные и нечетные суммы ряда имеют тот же предел, следовательно, ряд сходится. Теорема доказана.

По знакочередующемуся ряду можно построить соответствующий ему положительный ряд u₁ + u₂ + u₃ + u₄ + u_n +.... Если такой положительный ряд сходится, то знакочередующийся ряд называют абсолютно сходящимся, в противном случае ряд называют условно сходящимся. В абсолютно сходящемся ряде члены ряда можно переставлять без потери сходимости, в условно сходящемся ряде перестановка членов ряда запрещена, т.к. она может привести к потере сходимости.

Глава 8. Степенные ряды

Функциональнымрядом называется ряд, членами которого являются функции от аргумента x

u₁(x) + u₂(x) + u₃(x) +... + u_n(x) +... = 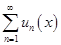(8.1)

Если в членах ряда (8.1) зафиксировать значение аргумента x=x₀, то получим числовой ряд

u₁(x₀) + u₂(x₀) + u₃(x₀) + u_n(x₀) +.... (8.2)

Если при x=x₀ числовой ряд (8.2) сходится, то x₀ называется точкой сходимости ряда (8.1).

Областью сходимости функционального ряда называется множество всех точек сходимости этого ряда. Если значение x₀ принадлежит области сходимости ряда (8.1), то можно говорить о сумме этого ряда в точке x=x₀:

u₁(x₀) + u₂(x₀) + u₃(x₀) + u_n(x₀) +... = S(x₀).

Таким образом, значение суммы функционального ряда зависит от значения переменной x, т.е. сумма функционального ряда сама является функцией переменной x.

Степенным рядом по степеням x называется функциональный ряд вида

а₀ + а₁x + а₂x² +... а_nxⁿ +... = 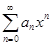(8.3)

где а₀, а₁,... а_n,... не зависят от переменной x и называются коэффициентами этого ряда.

Степенной ряд (8.3) всегда сходится, по крайней мере, в точке x =0. При любых конкретных x=x₀ ряд (8.3) превращается в числовой ряд

а₀ + а₁x₀ + а₂x₀² +... а_n x₀ⁿ +... (8.4)

Степенной ряд (8.3) сходится в точке x₀ абсолютно, если сходится ряд образованный из модулей членов числового ряда (8.4)

½а₀½ + ½а₁x₀½ + ½а₂x₀²½ +... ½а_n x₀ⁿ½ +....

Нахождение области сходимости степенного ряда. Найдем область сходимости ряда (8.3), используя признак Даламбера для положительных числовых рядов. По этому признаку ряд (5.3) сходится, если

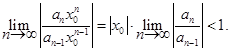
Следовательно, по признаку Даламбера ряд (8.3) заведомо сходится при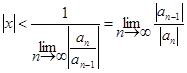

и расходится при .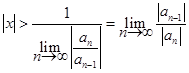

Величина 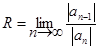(8.5)

называется радиусом сходимости ряда (8.3). Ряд заведомо сходится в интервале ½x½ < R или -R < x < R, который называется интервалом сходимости.

Признак Даламбера ничего не говорит о сходимости ряда в точках х = 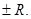. В этих точках сходимость ряда исследовать отдельно.

Исследовать степенной ряд на сходимость означает найти его интервал сходимости и установить сходимость или расходимость ряда в граничных точках интервала, т.е. при x = R и x = -R.

Пример 1. Исследовать на сходимость степенной ряд

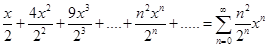
Решение. Используя формулу (8.5), имеем

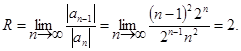
Интервал сходимости данного ряда характеризуется неравенством ½x½ < 2. Исследуем сходимость ряда в граничных точках x=±2. Очевидно, что

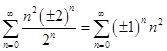
Оба эти ряда расходятся, так как не выполняется необходимое условие сходимости численных рядов. Следовательно, область сходимости данного степенного ряда совпадает с интервалом сходимости.

Пример 2. Найти область сходимости следующего ряда

1 + x + 2²x² + 3³x³ +... + nⁿxⁿ +... = 1 +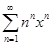

Решение. По формуле (5.5) найдем

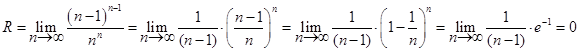
Следовательно, ряд сходится только в одной точке x =0.

Пример 3. Найти область сходимости следующего ряда:

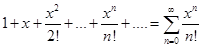
Решение. Так как

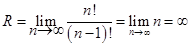
то ряд сходится при всех конечных значениях x, т.е. -¥ < x <¥.

Дата добавления: 2014-11-18