Структурный анализ механизмов

Проектирование и исследование Рычажных механизмов

Учебном процессе

Цели и задачи дисциплины, ее место в

Цель преподавания дисциплины.

Теория механизмов и машин – общепрофессиональная дисциплина, призванная заложить у студентов научные основы создания высокоэффективных машин и механизмов в современной технике. Теория механизмов и машин (далее ТММ) содержит основные сведения по анализу и синтезу механизмов различных структурных групп и разнообразного функционального назначением с применением графических, графоаналитических и аналитических методов.

Теория механизмов и машин наряду с теоретической механикой, математикой, физикой, инженерной графикой, информатикой и др. дисциплинами, представляет собой основу общетехнической подготовки дипломированного специалиста.

Основными задачами курса являются:

· формирование инженерного мышления будущих специалистов;

· изучение методов анализа и синтеза механизмов разнообразного назначения;

· изучение методов кинематического, силового и динамического анализа машин и механизмов;

· изучение основ проектирования механизмов с низшими и высшими кинематическими парами;

· изучение вопросов передачи работы и мощности, коэффициента полезного действия механизмов в целом и их составных частей;

· изучение вопросов движения и активного воздействия на движение механизмов для обеспечения требуемого закона;

· изучение машин-автоматов, промышленных роботов и т.д.

В результате изучения ТММ студент должен иметь представление:

· о структурном строении механизма;

· о методах анализа и синтеза механизмов;

· о современных методах проектирования кинематических схем типовых механизмов;

· о рычажных, кулачковых и зубчатых механизмах;

· о статике и динамике машин;

· о трении в кинематических парах и фрикционных передачах;

· коэффициенте полезного действия механизмов и машин;

· о движении механизмов под действием заданных сил, неравномерности и регулировании хода машин;

· о методах виброзащиты и уравновешивания машин;

· о машинах-автоматах и промышленных роботах.

Для изучения ТММ студент должен освоить дисциплины "Высшая математика", "Физика", "Начертательная геометрия. Инженерная графика", "Информатика" и др.

Любая машина состоит из механизмов. Механизм - это механическая система тел, предназначенных для преобразования движения одного или нескольких тел в требуемое движение других тел. Механизм представляет собой совокупность тел, связанных между собой подвижно. Каждое из тел, входящих в состав механизма, называется звеном.

Звенья разделяются на подвижные, неподвижные, жесткие, упругие, гибкие, жидкие или пневматические, а также входные, выходные и промежуточные. Все неподвижные детали, входящие в состав одного механизма, называются стойкой. Входным (ведущим) называется звено, которому сообщается движение, преобразуемое механизмом в требуемое движение других звеньев. Выходным - называется звено, совершающее движение, для выполнения которого предназначен механизм. Остальные звенья являются промежуточными.

Подвижное соединение двух соприкасающихся звеньев называется кинематической парой. Если элементом кинематической пары является линия или точка, то такая кинематическая пара называется высшей кинематической парой; если элементом кинематической пары является поверхность, то такая кинематическая пара называется низшей кинематической парой. К низшим парам принадлежат: вращательная, поступательная, винтовая, цилиндрическая, сферическая и плоскостная. У низших кинематических пар возможно только скольжение элементов. У высших кинематических пар возможно скольжение и качение.

Пока звенья не соединены в кинематическую пару, то каждое звено имеет 6 степеней свободы: три возможных поступательных перемещения вдоль трех неподвижных координатных осей X, Y, Z и три вращательных движения вокруг этих осей.

Ограничения, наложенные на относительное движение звеньев, называют связями. Комбинация связей, зависящая от конструктивной формы элементов кинематической пары, приводит к тому или иному виду относительного движения.

Число условий связи S, наложенных на относительное движение каждого звена кинематической пары, может располагаться в пределах от 1 до 5, т.е.: .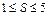

Число степеней свободы Н звена кинематической пары в относительном движении звеньев:

Н = 6 - S, (2.1)

где S -число условий связей, налагаемое элементами кинематической пары на относительное движение звеньев.

Все кинематические пары делятся на классы в зависимости от числа условий связи, налагаемых ими на относительное движение их звеньев. Так как условий связи может быть от 1 до 5, то и число классов пар равно 5, в соответствии с чем мы имеем кинематические пары I, II, III, IV и V классов. К первому классу относятся пары с S =1. Ко второму классу относятся пары с S =2 и т.д.

Примеры некоторых наиболее распространенных кинематических пар с их условными обозначениями приведены в таблице 2.1. Стрелками показаны возможные независимые движения одного звена относительно другого.

Совокупность некоторого числа звеньев, сочлененных при помощи кинематических пар, называется кинематической цепью. Все кинематические цепи подразделяются на плоские и пространственные. В плоской кинематической цепи точки всех звеньев перемещаются в параллельных плоскостях. В пространственных цепях точки описывают либо пространственные кривые, либо плоские кривые, расположенные в различных плоскостях.

Степенью подвижности кинематической цепи называют число ее степеней свободы относительно неподвижного звена.

Пусть имеется система из "n" свободных звеньев. Каждое звено имеет 6 степеней свободы, а все "n" звеньев в сумме (6∙n) степеней свободы. Если соединить эти звенья кинематическими парами, каждая из них наложит на относительное движение звеньев определенное количество связей, т.е. отнимет у системы часть степеней свободы. Пусть в соединении звеньев системы имеется: пар V кл. - Р₅., пар IV кл. - Р₄,.., пар I кл. -Р₁. Каждая пара V кл. накладывает на движение системы 5 связей, а все пары V кл. - 5∙P₅ - связей. Аналогично, все пары IV кл. накладывают- 4∙Р₄ связей, III кл. - 3∙P₃ связей, II кл. -2∙P₂. связей, I кл. - 1∙Р₁ связей.

Таблица 2.1. Классификация кинематических пар

Число связей	Рисунок	Возможные движения
S=1 W=5 1
S=2 W=4 2
S=3 W=3 3
S=4 W=2 4
S=5 W=1 5

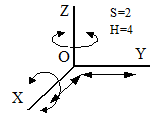
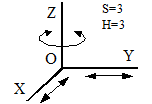
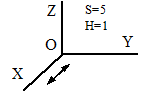
Общее число связей:

S = 5∙P₅ + 4∙P₄ + 3∙P₃ + 2∙Р₂ + 1∙Р₁.

Тогда степень подвижности системы с учетом всех связей

W = 6∙n - 5∙P₅ - 4∙P₄ - 3∙P₃ - 2∙Р₂ - 1∙Р₁. (2.2)

Полученное выражение называется структурной формулой пространственной кинематической цепи. В плоской цепи каждое звено имеет 3 степени свободы, т.к. на движение всех звеньев уже наложены три общие связи. Все звенья этой системы имеют [(6-3)∙n] степеней свободы. Каждая кинематическая пара накладывает на относительное движение звеньев на три связи меньше, чем в пространстве. С учетом сказанного

W = 3∙ n - 2∙ P ₅ - P ₄. (2.3)

Это выражение называют структурной формулой плоской кинематической цепи или формулой Чебышева.

В плоской кинематической цепи могут быть только одноподвижные кинематические пары V кл. и двухподвижные пары IV кл.

Простейшие рычажные механизмы (рис. 2.1) имеют четыре звена, одно из которых стойка. В зависимости от характера движения и назначения остальные звенья имеют определенные названия. Звено 1, совершающее полный оборот, называется кривошипом. Звено, совершающее сложное плоскопараллельное движение, называется шатуном (рис. 2.1, а и 2.1, б). Звено, совершающее возвратно-поступательное движение – ползун (рис. 2.1, а). Звено, совершающее качательное движение – коромысло (рис. 2.1, б). Звено, являющееся подвижной направляющей для ползуна, называется кулисой, а ползун, образующий с кулисой поступательную кинематическую пару, в этом случае именуется кулисным камнем (рис. 2.1, в).

Четырехзвенные рычажные механизмы преобразуют вращательное движение кривошипа в неравномерное вращательное, возвратно-поступательное или сложное движение шатуна. Если входным звеном является ползун, то механизмы преобразуют поступательное движение в неравномерное вращательное движение кривошипа.

а)

б)  

в)

Рис. 2.1. Простейшие четырехзвенные рычажные механизмы

а - кривошипно-ползунный механизм; б - шарнирный четырехзвенник;
в - кулисный механизм

В рассмотренных рычажных механизмах входным звеном обычно является кривошип, к которому присоединяются двухповодковые группы Ассура 1, 2, 3 вида [1]. Данные механизмы согласно классификации И.И. Артоболевского являются механизмами II класса.

Строение механизмов (рис. 2.1) описывается следующей структурной формулой

I (4-1) → II (2-3) (2.4)

Дата добавления: 2014-11-18