Силовой анализ механизмов

При проведении кинематического анализа мы предполагали движение входного звена (кривошипа) известным и движение выходных звеньев исследовали в зависимости от заданного движения входного звена. При этом силы, действующие на звенья механизма, и силы, возникающие при его движении, не изучались. Таким образом, при кинематическом анализе исследование движения механизма проводилось с учетом только структуры механизма и геометрических соотношений между размерами его звеньев.

Динамический анализ механизмов в общем случае имеет своими задачами:

· изучение влияния внешних сил, сил веса звеньев, сил инерции на звенья механизма на кинематические пары и неподвижные опоры и установление динамических нагрузок, возникающих при движении механизма;

· изучение режима движения механизма под действием заданных сил и установление способов, обеспечивающих заданные режимы движения механизма.

В курсовом проекте проводится силовой расчет механизма, состоящий в определении реакций связей в кинематических парах, сил инерции звеньев и других сил, возникающих при движении механизма. Трение в кинематических парах не учитывается.

Силовой расчет механизма проводится методом, основанным на использовании уравнений равновесия твердого тела. Сущность этого метода сводится к применению уравнений равновесия в форме Даламбера при решении задач динамики.

2.3.1. Определение сил, действующих на звенья механизма

В процессе работы машины к ее звеньям приложены заданные внешние силы, к которым относятся: движущая сила, сила технологического (полезного) сопротивления, силы тяжести звеньев, механические или добавочные сопротивления, а также силы инерции, появляющиеся в результате неравномерного движения звена. Неизвестными силами будут реакции связей, действующие на элементы кинематических пар.

Шарнирно-рычажные механизмы состоят из стержней и ползунов. Звенья – стержни рассматриваются однородными, имеющими вес 1 ^го метра длины, обозначаемый q.

Вес звеньев– стержней определяем по формуле

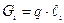, (2.18)

где ℓ_i – длина звена.

Вес звеньев стержней и ползунов прикладываем в центре тяжести и направляем вертикально вниз (рис. 2.8, а). Поскольку звено АВ – однородный стержень, центр его тяжести (точка S) находится в его геометрической середине.

Вес ползунов приложен в их центре тяжести. В кривошипно-кулисных механизмах весом кулисного камня пренебрегаем, считаем его малым по сравнению с весом других звеньев механизма.

Силы инерции – силы, распределенные по звену и являющиеся результатом ускоренного его движения.

При определении усилий в кинематических парах и характера движения механизма оперируют статически эквивалентными системами и вместо распределенных сил инерции пользуются их равнодействующими.

Сила инерции ползуна, движущегося прямолинейно, равна по модулю произведению массы ползуна (m _i) на его ускорение (a _{S i} ) и направлена противоположно ускорению ползуна (рис. 2.9, а).

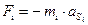, (2.19)

где 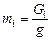; g – ускорение свободного падения.

а)		б)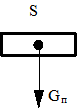
Рис 2.8. Силы тяжести звеньев механизма а - стержень; б - ползун
а)		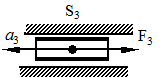б)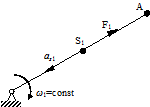
в)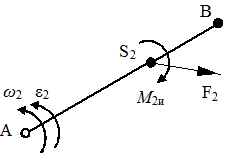
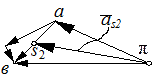
г)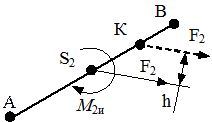
Рис. 2.9. Силы инерции звеньев механизма а - ползун; б - кривошип; в - шатун; г - определение точки приведения

Сила инерции кривошипа, вращающегося с постоянной угловой скоростью ω₁, направлена по звену к центру вращения (рис. 2.9, б) и определяется по формуле

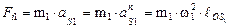. (2.20)

В общем случае, когда звено совершает плоское движение, инерционная нагрузка приводится к силе инерции и инерционному моменту (рис. 2.9, в).

Сила инерции шатуна направлена в сторону, противоположную вектору 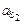(рис. 2.9, в) и равна по модулю

.

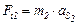Момент сил инерции шатуна направлен противоположно угловому ускорению ε₂ и равен по модулю

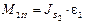, (2.21)

где 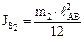– момент инерции шатуна относительно центра тяжести точки S₂.

Силу инерции F ₂ и пару сил с моментом инерции М _2И можно заменить одной силой F ₂, приложенной в точке К, называемой точкой приведения. Положение точки К определяется графически из условия, что плечо h силы F ₂ равно (рис. 3.2, г)

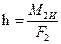. (2.22)

Силы полезного сопротивления – представляют собой силы в рабочих машинах, появляющиеся при непосредственном выполнении технологического процесса: при резании, штамповке металлов, подъеме груза и т.п. В точных механизмах силами полезного сопротивления являются противодействующие усилия и моменты, создаваемые упругими элементами приборов, отсчетных устройств и др. В курсовом проекте величина, направление и точка приложения силы полезного сопротивления F_п.с. заданы.

Силы реакции в кинематических парах – представляют силы, действующие со стороны одного звена на другое, они обозначаются буквой R с соответствующими индексами. Например: R ₁₂ – сила, с которой звено 1 действует на звено 2. Учитывая равенство действия и противодействия, имеем

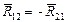. (2.23)

Направление сил реакции в низших кинематических парах зависит от характера соединения звеньев. Во вращательной паре (рис. 2.10, а) линия действия реакции проходит через ось вращения кинематической пары, модуль и направление реакции – неизвестны.

В поступательной паре в общем случае реакция сводится к реактивной силе R ₂₁, приложенной в центре ползуна перпендикулярно направляющей 2 и реактивному моменту М ₂₁. При этом неизвестны модуль силы реакции и величина момента (рис.2.10, б).

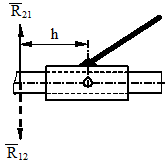
Реактивные силы R ₂₁ и момент М ₂₁ могут быть приведены к одной силе (рис. 2.10, в), при этом неизвестны величина силы R ₂₁ и точка ее приложения – плечо h.

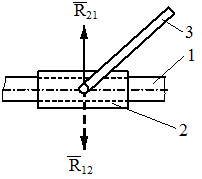
В частном случае, когда ползун 1 с шатуном 3 соединены шарнирно, как показано на рисунке 2.10, г, реакция приложена в середине ползуна и направлена перпендикулярно направляющей. Модуль реактивной силы при этом неизвестен R ₂₁.

В основу метода определения реакций в кинематических парах положен принцип Даламбера, согласно которому динамическая система условно сводится к статической системе путем приложения к звеньям механизма сил инерции и моментов сил инерции.

Поскольку в механизме группы Ассура являются статическими определимыми, то расчет каждой группы проводится в отдельности. Первоначально рассматриваются группы, наиболее удаленные от входного звена.

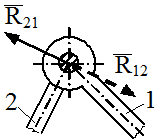
а)	б)
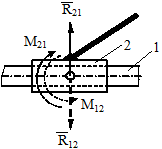
в)	г)

Рис. 2.10. Определение реакций в кинематических парах

а - вращательная пара; б, в, г - поступательная кинематическая пара

Уравнения равновесия сил для определения реакций в кинематических парах групп Ассура второго класса представлены в таблице 2.3. При использовании этой таблицы следует иметь в виду, что на расчетных схемах не указана сила полезного сопротивления (F _п.с.).

Силовые многоугольники строятся с использованием масштабного коэффициента сил μ_F.

Таблица 2.3. Уравнения равновесия для определения реакций в кинематических парах

групп Ассура II класса

Вид группы	Расчетная схема	Определяемый параметр	Условие равновесия	Метод решения	Уравнения равновесия	Результат решения
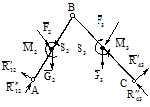
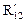
			звена 2	Аналитический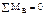
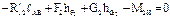
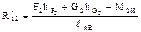
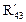
	звена 3	Аналитический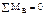
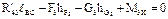
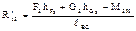
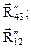
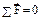
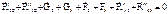
	группы	Графический		Из плана сил
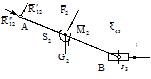
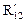
			звена 2	Аналитический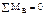
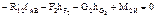
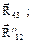
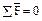
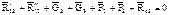
	группы	Графический		Из плана сил
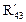
			группы	Аналитический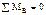
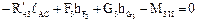
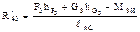
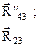
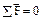
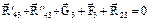
	звена 3	Графический		Из плана сил
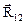
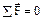
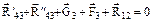
	группы	Графический		Из плана сил

2.3.2. Определение уравновешивающей силы и уравновешивающего момента

Сила F _у и момент М _у, приложенные к входному звену, уравновешивающие действия всех остальных внешних сил и моментов, действующих на механизм, называются уравновешивающими.

Если входное звено приводится в движение от вала электродвигателя через муфту, то оно уравновешивается моментом М _у; если вращение осуществляется через зубчатую или фрикционную передачу – на входное звено действует уравновешивающая сила F _у. Сила F _у направлена перпендикулярно кривошипу.

Уравновешивающая сила и момент связаны соотношением

М _у= F _у∙ℓ, (2.24)

где ℓ – плечо силы F _у – расстояние от оси кривошипа до точки приложения уравновешивающей силы, обычно ℓ=ℓ₁, м.

В курсовом проекте уравновешивающую силу необходимо определять двумя способами.

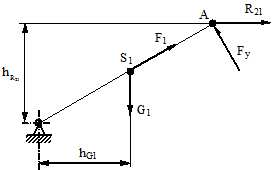
Первый способ. Заключается в определении из условия равновесия сил, действующих на кривошип (рис. 2.11)

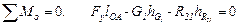, (2.25)

где R ₂₁ – сила, с которой шатун действует на кривошип; 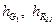– плечи соответствующих сил, которые определяются графически

Тогда

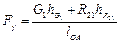. (2.26)

Второй способ. Для нахождения уравновешивающей силы используют теорему Н.Е. Жуковского о жестком рычаге " Если какой-либо механизм под действием сил 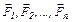находится в равновесии, то в равновесии и повернутый на 90⁰ план скоростей, рассматриваемый как жесткий рычаг, поворачивающийся вокруг полюса Р и нагруженный теми же силами 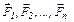, которые приложены в одноименных точках повернутого плана скоростей ".

  Рис. 2.11. Определение уравновешивающей силы

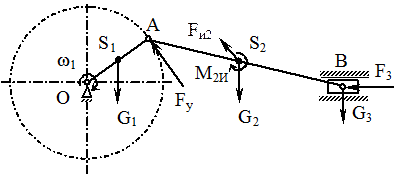
Если задан механизм и все силы, приложенные к нему (рис. 2.12, а), а также построен план скоростей механизма (рис. 2.12, б), то для нахождения уравновешивающей силы поступают следующим образом:

а) строят повернутый план скоростей механизма: план скоростей механизма закрепляют в точке Р и поворачивают относительно полюса на 90⁰ по вращению ведущего звена ω₁ (рис. 2.12, в);

б) в одноименные точки повернутого плана скоростей с кинематической схемы механизма переносят параллельно самим себе все действующие силы, включая силы веса, инерции, полезного сопротивления и искомую уравновешивающую силу, которая направляется перпендикулярно отрезку . Необходимо иметь в виду, что если к звену механизма приложен внешний момент М_2И (рис. 2.12, г), то его заменяют парой сил 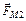. Силы 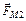направлены перпендикулярно звену и численно равны

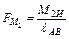, (2.27)

где ℓ _АВ – плечо пары сил. Силы 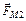переносят в соответствующие точки повернутого плана скоростей;

в) принимают повернутый план скоростей за рычаг с точкой опоры в полюсе Р; записывают уравнение равновесия рычага, из которого находят величину искомой уравновешивающей силы

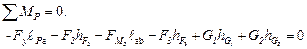. (2.28)

Откуда

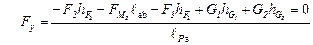. (2.29)

Как видно в формулах (3.26) и (2.29) все слагаемые содержат сомножители, представляющие плечи сил, измеренные на повернутом плане скоростей, поэтому, вычисляя F _y по формулам (2.26) и (3.29), нет необходимости учитывать масштабный коэффициент плана входного звена и скоростей механизма.

После определения уравновешивающей силы двумя рассмотренными способам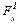и и 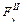, вычисляют среднее ее значение

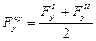(2.30)

и определяют относительную ошибку вычислений

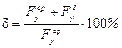, (2.31)

которая не должна превышать 10 %.

Если δ>10 %, то необходимо уточнить графические построения и проверить условия равновесия. Следует также иметь в виду то, что графоаналитический метод решения, используемый для определения 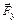, требует аккуратных графических построений, существенно влияющих на точность конечного результата.

Силовой расчет механизма заканчивается определением уравновешивающего момента М _у и мгновенной мощности движущих сил Р, величины которых вычисляют по формулам

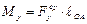, (2.32)

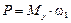(2.33)

а)
б)	в)
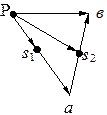
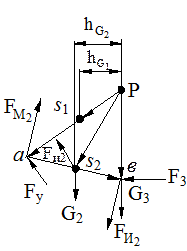
г

Рис. 2.12. Определение уравновешивающей силы

с помощью рычага Жуковского

а - план механизма; б - план скоростей; в - рычаг Н.Е. Жуковского;
г - схема замены момента М_2И парой сил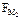

Дата добавления: 2014-11-18