Примеры расчетов рычажных механизмов

2.4.1. Шарнирный четырехзвенник

Рассчитать шарнирно-рычажный механизм по следующим исходным данным: длина кривошипа ℓ ₁=0,050 м, длина шатуна ℓ ₂=0,12 м, длина коромысла ℓ _св= ℓ _вд=0,135 м, расстояние между центрами вращения ℓ ₄= ℓ _АС=0,140 м, угловая скорость ω=10 с^-1, угол поворота кривошипа φ=45^о, удельная масса 1 погонного метра q=200 н·м^-1, сила полезного сопротивления F _п.с.=0,7 кН. Сила полезного сопротивления приложена в точке D механизма и направлена противоположно вектору скорости υ_Д.

2.4.1.1. Структурный анализ и построение плана механизма

Выбираем масштабный коэффициент длины μ_ℓ=0,0002 м/мм. Вычерчиваем кинематическую схему механизма и показываем на ней угол качания коромысла (рис. 2.13, а).

Число степеней подвижности механизма определяем по формуле П.Л. Чебышева

W = 3· n - 2· P₅ - P ₄,

где n = 3; Р ₅ = 4; Р ₄ = 0.

W = 3·3 - 2·4 - 0 = 1

В данном механизме ведущим является кривошип 1, к которому присоединена двухповодковая группа Ассура (2 – 3) 1 ^го вида. Механизм, согласно классификации И.И. Артоболевского, является механизмом II класса.

Строение механизма описывается структурной формулой

I (4 – 1) → II (2 – 3)

Изображаем план механизма при φ=45^о, μ_ℓ=0,0002 м/мм (рис. 2.13, б).

2.4.1.2. Определение скоростей точек

Определяем скорости точек А, В, D, S₁, S₂, S₃ с помощью плана скоростей механизма (рис. 2.13, в).

=10·0,05=0,5 м/с,

.

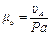
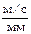а)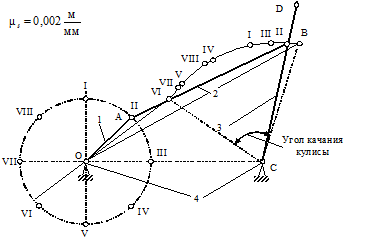
б)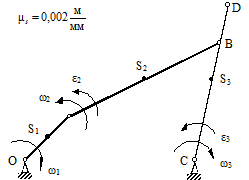
в)

Рис. 2.13. Пример расчета шарнирно-рычажного механизма

а - план положений механизма и определение крайних положений кулисы;
б - схема механизма в заданном положении; в - планы скоростей и ускорений

Для определения скорости точки В используем векторные уравнения, представленные в таблице 2.2.

.

Определяем угловые скорости звеньев:

Определяем скорости точек S₁, S₂, S₃ и D из теоремы подобия для скоростей

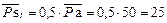мм;

= 25·0,01 = 0,25 м/с;

=0,5·35 = 17 мм;

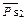=35 мм; 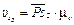= 0,35·0,1 = 0,35 м/с;

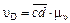= 45·0,01 = 0,45 м/с;

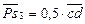=0,5·0,45 = 22 мм;

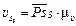=22·0,01 = 0,22 м/с.

2.4.1.3. Определение ускорений точек

Определяем ускорения точек А, В, D, S₁, S₂ и S₃ с помощью плана ускорений механизма (рис. 2.13, в).

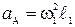=10²·0,05=5,0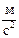

Для определения ускорения точки В используем векторные уравнения представленные в таблице 2.2.

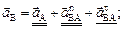
=2,9²·0,12 = 1,0 ;

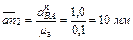
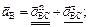
=3,3²·0,075 = 0,8 ;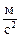

;

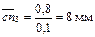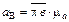=58·0,1 = 5,8 .

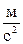Определяем угловые ускорения звеньев

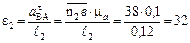с^-2;

с^-2.

Определяем ускорения точек S₁, S₂, S₃ и D из теоремы подобия для ускорений

=0,5·50 = 25 мм;

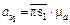=25·0,1 = 2,5 ;

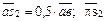=50 мм;

=50·0,1 = 5,0 ;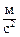

=104 мм;

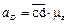=104·0,1 = 10,4 ;

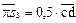=0,5·104 = 52 мм;

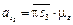=52·0,1 = 5,2 .

2.4.1.4. Определение уравновешивающей силы

Определяем силы, действующие на звенья механизма.

1) силы веса и массы звеньев:

G ₁=q· ℓ ₁=200·0,05=10 Н;

G ₂=q· ℓ ₂=200·0,12=24 Н;

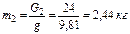
G ₃=q· ℓ ₃=200·0,135=27 Н;

Силы веса G₁, G₂, G₃ прикладываем в точках S₁, S₂, S₃ соответственно и направляем вертикально вниз (рис. 2.14, а, в).

2) силы инерции звеньев:

F ₁= =1,02·2,5 = 2,6 Н;

F ₂= 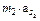= 2,44·5,0 = 12,2 Н;

F ₃= 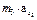= 2,8·5,2 = 14,6 Н

Силы инерции F₁, F₂, F₃ прикладываем в точках S₁, S₂, S₃ и направляем противоположно ускорениям соответствующих точек механизма.

3) моменты сил инерции

= 2,9·10^-3 кг·м²;

М _2И = 2,9·10^-3·32 = 0,092 Н·м;

= 4,2·10^-3 кг·м²;

М _3И = 4,2·10^-3·76 = 0,323 Н·м

Моменты М _2И и М _3И направляем противоположно угловым ускорениям звеньев ε₂ и ε₃.

4) определяем реакции в кинематических парах

Изображаем в масштабе μ_ℓ =0,002 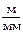план группы звеньев (2–3). На плане указываем действующие силы и моменты сил G₂, G₃, F_п.с., F₂, F₃, М_2И и М_3И (рис. 2.14, а). Неизвестные реакции раскладываем на составляющие: нормальную 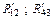и касательную .

Для определения реакций в кинематических парах используем уравнения равновесия, представленные в таблице 2.3.

Рассматриваем равновесие звена 2:

;

;

;

.

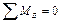Плечи сил здесь и в дальнейшем определяем графически (рис. 2.14, а).

Рассматриваем равновесие звена 3:

;

.

;

.

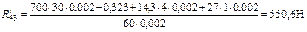а)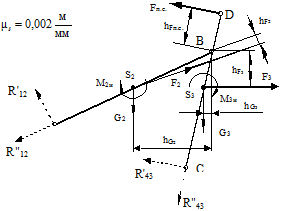
б)
в)		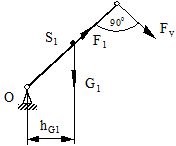г)

Рис. 2.14. Кинетостатическое исследование механизма

а - группа Ассура, б - план сил, в - входное звено, г - рычаг Жуковского

Для определения касательных составляющих реакций и строим силовой многоугольник сил, действующих на группу звеньев (2–3). Выбираем масштаб сил μ_F=20 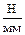. В силовом многоугольнике силы, представляемые в выбранном масштабе отрезками меньше 1 мм, выродились в точку.

Из силового многоугольника с учетом масштаба сил имеем

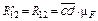=70·20 = 1400 Н;

=56·20 = 1120 Н.

Рассматриваем равновесие ведущего звена 1.

На ведущее звено действуют силы: (рис. 2.14, в).

;

;

.

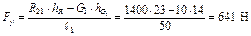Определяем уравновешивающую силу с помощью рычага Жуковского.

Строим повернутый на 90⁰ относительно точки Р план скоростей механизма.

Моменты сил инерции М _2И и М _3И заменяем парами сил:

;

.

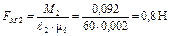Пару сил прикладываем перпендикулярно шатуну в точках А и В, а пару сил – перпендикулярно коромыслу в точки С и D. На повернутый план скоростей в соответствующие точки параллельно самим себе переносим силы, действующие на механизмы (рис. 2.14, г).

Рассматриваем равновесие рычага Жуковского относительно полюса Р_υ.

.

,

.

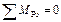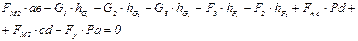
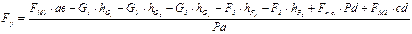Среднее значение уравновешивающей силы

Относительная ошибка вычисления уравновешивающей силы

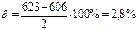
Определяем уравновешивающий момент

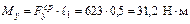
Определяем мгновенную мощность движущих сил

Р = М _у ∙ ω₁ = 31,2∙10 = 312 Вт.

2.4.1.5. Кинематические диаграммы строим в соответствии с методикой, изложенной в п. 2.2.4. Пример диаграмм показан на рис. 2.7.

2.4.2. Кинематическое исследование кулисного механизма

Рассчитать шарнирно-рычажный механизм по следующим исходным данным: ℓ _01А=0,4 м, ℓ _02В=2 м, ℓ _ВС=0,9 м, ℓ _а=1,2 м, ℓ _b=1,4 м, n ₁=300 мин^-1, φ=240^о. Схема механизма показана на рис. 2.15.

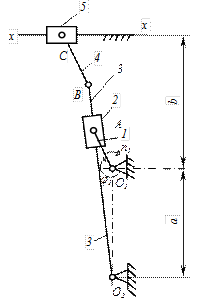
Рис. 2.15. Схема кулисного механизма

2.4.2.1. Построение плана и крайних положений механизма

Построение плана начинают с определения длин отрезков изображающих звенья механизма на чертеже. Величина масштабного коэффициента должна приниматься такой, чтобы отрезки, изображающие звенья механизма на плане, не превышали 150 мм. Приняв величину отрезка ОА, изображающего на плане кривошип, равным 20 мм получим:

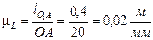- масштабный коэффициент длин.

Тогда звенья механизма на плане изобразятся отрезками:

О₂В = 100 мм; ВС= 45 мм;

а = 60 мм; b = 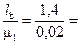70 мм;

Рис. 2.16. План и структурные группы механизма

Вычерчивание механизма (рис. 2.16, а) проводим в следующем порядке. В произвольном месте чертежа выбираем точку О₂, от которой откладываем вертикально вверх расстояние а = 60 мм и намечаем точку О ₁. На расстоянии b = 70 мм от точки О₁ проведем горизонтальную прямую x-x, на которой будет расположена точка С. Из точки О₁ под углом 240° отложим отрезок О₁А = 20 мм. Через точки О₂ и А проведем отрезок О₂В = 100 мм. Затем раствором циркуля, равным отрезку ВС = 45 мм, сделаем засечку на горизонтальной прямой x-x и получим точку С. Таким образом будем иметь план механизма.

Для заданного механизма крайние положения выходного звена 5 (ползуна) будут определяться крайним левым и крайним правым положениями звена 3 (кулисы).

Для нахождения этих положений радиусом О₁А опишем окружность вокруг точки О₁, затем из точки О₂ проведем касательные к этой окружности и наметим точки А_Л и А_Пр (точки касания), а также точки В_Л и В_Пр (рис. 2.17, а). Далее, используя метод засечек, найдем крайние положения звена 5. Для этого раствором циркуля, равным отрезку ВС, из точек В_Пр и Вл на прямой x-x сделаем засечки, которые и определят точки С_Пр и С_Л. Расстояние между этими точками S называется ходом выходного звена. Если выходным звеном является кулиса или коромысло определению подлежат их углы качания ψ_max.

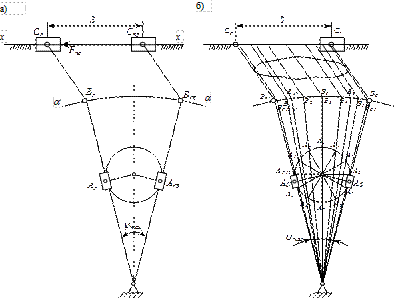
Рис. 2.1 7. Построение крайних положений механизма

2.4.2.2. Определение степени подвижности и класса механизма

Рассматриваемыймеханизм состоит из пяти подвижных звеньев и стойки. Звено 1 - Кривошип, вращающееся звено рычажного механизма, совершающее полный оборот относительно неподвижной оси. В механизмах второго класса является ведущим звеном; 2 – кулисный камень, звено, имеющее подвижную направляющую; 3 – кулиса, звено, служащее направляющей для кулисного камня; 4 – шатун, звено, совершающее плоско-параллельное движение и не образующее кинематических пар со стойкой; 5 – ползун, звено, перемещающееся по неподвижной направляющей (стойке); 0 – неподвижное звено-стойка.

Звенья 0 – 5 соединены между собой семью кинематическими парами V класса, представленными в таблице 2.4.

Таблица 2.4. Характеристика кинематических пар механизма.

Обозначение кинематической пары	Номера звеньев, образующих пару	Характер относительного движения звеньев	Класс кинематической пары
О А А В С С О	0 и 1 1 и 2 2 и 3 3 и 4 4 и 5 5 и 0 3 и 0	Вращательное Вращательное Поступательное Вращательное Вращательное Поступательное Вращательное	V- пятый V- пятый V- пятый V- пятый V- пятый V- пятый V- пятый

Степень подвижности механизма по формуле Чебышева П.Л.:

W =3 n – 2 P ₅ – P ₄=3·5 - 2·7 = 1,

где n – число подвижных звеньев, Р ₅ – число пар пятого класса, Р ₄ – число пар четвертого класса (Р ₄=0)

Для определения класса механизма разобьем его на группы Ассура. Разложение механизма на группы Ассура начинают с группы наиболее удаленной от начального механизма. Поэтому, прежде всего, отсоединяем группу Ассура, состоящую из звеньев 4 и 5, внутренней вращательной кинематической пары С (4, 5) и двух элементов кинематических пар В и С. Эта группа II класса, 2 порядка, 2 вида (рис. 2.16, б) Затем отсоединяем группу, состоящую из звеньев 3 и 2 (рис. 2.16, г.), внутренней поступательной кинематической пары А (2, 3) и трех элементов кинематических пар О₂, А, В. Это группа II класса, 2 порядка, (два свободных элемента для присоединения к механизму, а элемент В - для присоединения последующей группы), 3 вида. После отсоединения указанных групп остался исходный (начальный) механизм первого класса, состоящий из кривошипа 1, присоединенного к стойке кинематической парой О ₁ (рис. 2.16, в).

Структурная формула строения механизма запишется в виде:

I (0,1) ® II (2, 3) ® II (4, 5).

В целом рассматриваемый механизм относится ко II классу, что определяется классом наиболее сложной группы.

2.4.2.3. Построение траекторий точек

Траектории шарнирных точек были определены при построении крайних положений механизма: траектория точки А – окружность с радиусом r _А = О₁А, траектория точки В – дуга α-α с радиусом r _В = О₂В, траектория точки С – прямая х-х, ограниченная отрезком S (ходом ползуна). Для построения траекторий точек принадлежащих звеньям, например, точек, определяющих центр масс звеньев (точка S ₄ для шатуна 4) необходимо построить несколько положений механизма (чаще всего строят 12 положений) и на каждом из этих положений отметить соответствующую точку. Соединив плавной кривой отмеченные точки, получают искомую траекторию движения (рис. 2.17, б).

Для построения 12 положений механизма траекторию движения точки А (точка принадлежит ведущему звену 1 – кривошипу) разбивают на 12 частей. За начало отсчета принимают одно из крайних положений механизма, соответствующее началу рабочего хода, обозначают это положение цифрой 0. Следующие за ним по ходу движения положения обозначают по порядку цифрами 1…12 (при этом точки 0 и 12 – совпадают).

Промежуточные положения, например, соответствующие заданному углу φ, или второму крайнему положению механизма, обозначают номером предшествующей точки с добавлением штрихов (например, … 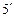и т.п.) Пример построения 12 положений механизма и траектории центра масс шатуна показан на

рис. 2.17, б.

2.4.2.4. Построение планов скоростей

Построение плана скоростей начинают с определения численного значения скорости точки А₁ кривошипа, который вращается с постоянной угловой скоростью ω₁

0,4 · 31,4 = 12,56 (м/с);

ω₁= (с^-1)

где n ₁ - частота вращения кривошипа, l _ОA - длина кривошипа.

Эта скорость направлена перпендикулярно оси звена О₁А в сторону вращения кривошипа. Задавшись длиной отрезка Ра = 62,8 мм, который будет изображать на плане скорость 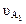точки 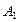, определим масштаб плана скоростей:

, .

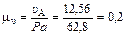Построение плана скоростей механизма показано на рис. 2.18, б. Из произвольной точки Р, принятой за полюс плана скоростей, перпендикулярно звену О₁А откладывают отрезок Ра. Скорости неподвижных точек О ₁ и О ₂ равны нулю, поэтому векторы Ро₁ и Ро₂ также равны нулю и, следовательно, точки о ₁ и о ₂ на плане скоростей совпадают с точкой Р (полюсом). Для скорости точки А ₃, принадлежащей звену 3, можно записать векторные уравнения

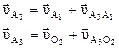, (2.34)

где 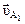- вектор скорости точки А ₁. 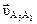, 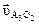- векторы относительных скоростей точки А ₃ во вращении вокруг точек А ₁ и О ₂.

Рис. 2.18. Построение планов скоростей и ускорений

Учитывая, что υ_О2 - скорость точки О ₂ равна нулю, выражения (2.34) запишем в виде:

. (2.35)

В этом и последующих выражениях известные по величинеи направлению составляющие будем подчеркивать двумя чертами, а известные только по направлению - одной чертой с указанием направления данной составляющей.

Таким образом, видим, что в выражение (2.35) входит известная по величине и линии действия скорость υ_А1 и известные только по направлению относительные скорости υ_А3А1 и υ_А3О2. В этом случае векторное уравнение (2.35) может быть решено графически. Для этого из точки а₁ плана скоростей проведем направление скорости 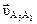параллельно звену О₂В (для рассматриваемого положения механизма), а из полюса р плана скоростей направление скорости 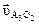, перпендикулярно звену О₂В. Пересечение этих направлений на плане скоростей даст нам точку а ₃, а вектор 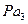в масштабеμ_υ будет изображать значение скорости точки А ₃ звена 3. Точка В принадлежит звену 3 также как и точки А ₃ и О ₂, поэтому скорость 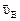может быть найдена по первому свойству плана скоростей (теорема подобия), на основании которого запишем:

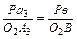, (2.36)

где О₂А₃ и О₂В - отрезки, взятые с плана механизма, а Ра₃ и Рв - отрезки с плана скоростей. Решая (2.36) относительно Рв, получим:

_.

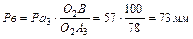Отрезок Р в в масштабе μ_υ изображает скорость точки υ_B кулисы, направленную в ту же сторону, что и скорость точки υ_А3.

Для нахождения скорости точки С запишем векторные уравнения

, (2.37)

где 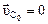- вектор скорости точки С, принадлежащей стойке х-х.

С учетом этого запишем:

. (2.38)

В выражении (2.38) две неизвестных по величине составляющих скорости точки С, т.е. это векторное выражение можно решить графически. Для этого из точки " в " плана скоростей проводим направление, перпендикулярное звену СВ, а из полюса плана скоростей направление, параллельное х-х. Пересечение этих направлений даст нам точку с, а вектор 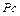в масштабе μ_υ скорость точки С. Полная картина плана скоростей показана на рис. 2.18, б. Скорость центра масс шатуна на плане скоростей определяется точкой S₄, находящейся на середине вектора вс (т.к. центр масс звена 4 расположен посередине шатуна ВС), аналогично, по первому свойству плана скоростей, находятся скорости центров масс (и любых других точек) остальных звеньев. Имея план скоростей и масштабный коэффициент μ_υ, определим:

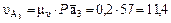(м/с);

(м/с);

(м/с);

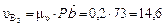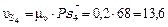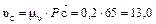(м/с);

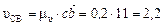(м/с);

(м/с)

Для определения угловых скоростей звеньев механизма воспользуемся вторым свойством плана скоростей. Угловые скорости кулисы (звено 3) w₃ и шатуна (звено 4) w₄ будут равны:

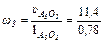=14,6 с^-1; 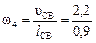= 2,4 с^-1

Угловая скорость кривошипа:

ω_-1= с^-1

Направления угловых скоростей ω₃ и ω₄ показаны стрелками на рис. 2.18, а. Дляих определения нужно векторы относительных скоростей с плана скоростей перенести параллельно самим себе в соответствующие точки плана механизма и посмотреть, в какую сторону они будут вращать интересующие нас звенья.

2.4.2.5. Построение планов ускорений

Построение плана ускорений выполняется в аналогичной последовательности. В начале определяют значение полного ускорения точки А ₁ кривошипа вращающегося с постоянной угловой скоростью ω₁ (следовательно а 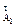= 0):

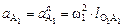= (31,4)² 0,4 = 396 (м /с²), (2.39)

Величину этого ускорения изображают на плане ускорений в виде отрезка p а ₁= 150,8 мм, отложенного из произвольно выбранной точки p – полюса плана ускорений. Вектор p а ₁ направлен параллельно звену О₁А от точки А ₁ к точке О ₁. Величина отрезка выбрана такой, чтобы получить удобное для расчетов значение масштабного коэффициента плана ускорений:

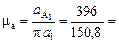2,5 ().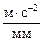

Для определения ускорения точки а _А3, составим векторные уравнения:

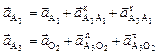. (2.39)

Принимая во внимание, что ускорение 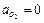выражение (2.39) перепишем в виде:

. (2.40)

Здесь 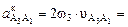2·14,6·4,4 = 128 (м/с²) – кориолисово ускорение, направление которого определяется поворотом вектора относительной скорости 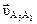на 90^О в направлении переносной угловой скорости ω₃. На плане ускорений величина 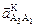изобразится отрезком а ₁ к:

= 51 (мм).

В выражении (2.9) - - относительное ускорение, имеющее направление относительного перемещения звеньев 2 и 3 (т.е. // О₂В), 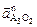- нормальная составляющая ускорения точки А ₃, направленная по звену А₃О₂ от точки А ₃ к точке О ₂ (к центру вращения звена), а - тангенциальная составляющая полного относительного ускорения точки А ₃. Вектор этой составляющей перпендикулярен звену А₃О₂.

14,6 · 0,78 = 167 (м/с²).

Таким образом, в уравнении (2.40) имеются только две составляющие неизвестные по модулю, но известные по направлению. Решим это уравнение графически. В соответствии с уравнением (2.40) из точки а₁ плана ускорений отложим вектор 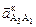в виде отрезка а₁к₁, изображающего кориолисово ускорение, и из полученной точки к₁ отложим направление относительного ускорения а // О₂В. Далее из полюса p отложим вектор нормальной составляющей полного относительного ускорения точки А ₃ в виде отрезка p n ₃= 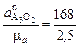= 68 (мм), направленного // звену О₂В к точке О ₂ (центру вращения звена 3). Из полученной точки n₃ проведем направление тангенциальной составляющей 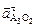. Пересечение этого направления и направления относительного ускорения - даст точку а₃, а вектор pа₃ в масштабе μ _а будет изображать полное ускорение точки А ₃ кулисы (рис. 2.18, в). Ускорение точки В находим используя свойство подобия планов:

,

откуда 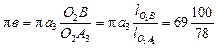= 88,6 мм.

Отложив этот отрезок из полюса плана ускорений, получим точку в. Численное значение ускорения этой точки

а_в= μ _а · pв = 2,5 · 88,6 = 220,1 м/с².

Для нахождения ускорения точки С составим векторные уравнения:

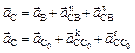, (2.41)

где 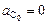, 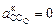и выражение (2.41) перепишется в виде:

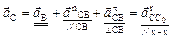, (2.42)

где 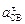- тангенциальная составляющая, имеющая направление перпендикулярное звену ВС, 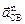- нормальная составляющая ускорения, направленная по звену СВ от точки С к точке В, и равная 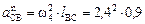= 5,2 (м/с²), 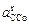- относительное ускорение, направленное вдоль направляющей х-х.

Уравнение (2.42) решаем графически, для чего из точки в плана ускорений отложим отрезок вn ₄, изображающий в масштабе μ _а нормальную составляющую :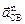

= 2,1 (мм).

Из точки n₄ проведем направление , а из полюса p направление 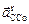. Пересечение этих направлений даст точку с, а вектор pс – в масштабе полное ускорение точки С ползуна 5. Перемножив величину отрезков (векторов) p а ₃, p в, p с, p s ₄, p s ₃ на величину масштабного коэффициента μ _а, получим численные значения ускорений соответствующих точек. Угловые ускорения звеньев:

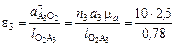= 32 ;

= 347 .

Результаты расчетов, полученные из планов скоростей и ускорений, сводим в таблицу 2.5.

Таблица 2.5. Абсолютные значения величин скоростей и

ускорений точек механизма

Скорости линейные υ, м/с и угловые ω, рад/с
Обозначение	υ A1	υ A3	υ B	υ C	υ A3A1	ω1	ω3	ω4
Величина	12,56	11,4	14,6		4,4	31,4	14,6	2,5
Ускорения линейные а, м/с^2 и угловые ε, рад/с^2
Обозначение	а А1	а А3	ав	а С	a S3	a S4	ε3	ε4
Величина			220,1

Дата добавления: 2014-11-18