Условия однозначности для процессов теплопроводности

Так как дифференциальное уравнение теплопроводности выведено на основе общих законов физики, то оно описывает явление теплопро­водности в самом общем виде. Поэтому можно сказать, что полученное дифференциальное уравнение описывает целый класс явлений тепло­проводности. Чтобы из бесчисленного количества выделить конкретно рассматриваемый процесс и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математи­ческое описание всех частных особенностей рассматриваемого процесса.

Эти частные особенности, которые совместно с дифференциальным урав­нением дают полное математическое описание конкретного процесса теплопроводности, называются условиями однозначности или краевыми условиями.

Условия однозначности включают в себя:

геометрические условия, характеризующие форму и размеры тела, в которых протекает процесс;

физические условия, характеризующие физические свойства среды и тела;

временные (начальные) условия, характеризующие распределение температур в изучаемом теле в начальный момент времени;

граничные условия, характеризующие взаимодействие рассматри­ваемого тела с окружающей средой.

Геометрическими условиями задаются форма и линейные размеры тела, в котором протекает процесс.

Физическими условиями задаются физические параметры тела 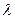, с, 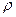и др. и может быть задан закон распределения внутренних источников теплоты.

Начальные условия необходимы при рассмотрении нестацио­нарных процессов и состоят в задании закона распределения темпера­туры внутри тела в начальный момент времени. В общем случае началь­ное условие аналитически может быть записано следующим образом:

при =0

t=f(x, y, z) (1.30)

В случае равномерного распределения температуры в теле началь­ное условие упрощается:

при =0

t=t₀=const. (1.31)

Граничные условия могут быть заданы несколькими спо­собами.

а) Граничные условия первого р о д а. При этом задается распределение температуры на поверхности тела для каждого момента времени:

t_c = f(x, y, z, ), (1.32)

где t_c—температура на поверхности тела; х, у, z— координаты поверх-, ности тела.

В частном случае, когда температура на поверхности является по­стоянной на протяжении всего времени протекания процессов тепло­обмена, уравнение (1.32) упрощается и принимает вид:

б) Граничные условия второго рода. При этом зада­ются значения теплового потока для каждой точки поверхности тела и любого момента времени.

Аналитически это можно представить следующим образом:

q_п =f(x, у, z, т), (1.33)

где q_п—плотность теплового потока на поверхности тела; х, у, z —координаты на поверхности тела.

В простейшем случае плотность теплового потока по поверхности и во времени остается постоянной:

q_п=q_о=const. (1.34)

Такой случай теплообмена имеет место, например, при нагревании различных металлических изделий в высокотемпературных печах.

в) Граничные условия третьего рода. При этом зада­ются температура окружающей среды t_ж и закон теплообмена между
поверхностью тела и окружающей средой. Граничное условие третьего
рода характеризует закон теплообмена между поверхностью и окружающей средой в процессе охлаждения и нагревания тела. Для описа-­
ния процесса теплообмена между поверхностью тела и средой используется закон Ньютона—Рихмана.

Процесс теплообмена между поверхностью тела и средой относится к очень сложным процессам и зависит от большого количества пара­метров. Согласно закону Ньютона—Рихмана количество теплоты, отдавае­мое единицей поверхности тела в единицу времени, пропорционально разности температур поверхности тела t_c я окружающей среды t_ж(t_c 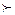t_ж)

q= 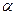(t_c—t_ж), (1.35)

где 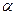— коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м²-К).

Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Численно он равен количеству теплоты, отдаваемому (или воспринимаемому) единицей поверхности в единицу времени при разности температур меж­ду поверхностью тела и окружающей средой, равной одному градусу.

Согласно закону сохранения энергии количество теплоты, которое отводится с единицы поверхности в единицу времени вследствие тепло­отдачи {уравнение (1.35)], должно равняться теплоте, подводимой к еди­нице поверхности в единицу времени вследствие теплопроводности из внутренних объемов тела {уравнение (1.10) *], т. е,

(1.36)

где n — нормаль к поверхности тела; индекс «с» указывает на то, что температура и градиент относятся к поверхности тела (при n = 0).

Окончательно граничное условие третьего рода можно записать в виде

(1.37)

Уравнение (1.37) по существу является частным выражением зако­на сохранения энергии для поверхности тела.

Коэффициент теплоотдачи зависит от большого числа факторов. Однако во многих случаях коэффициент теплоотдачи можно считать неизменным, поэтому мы будем в дальнейшем при решении задач тепло­проводности принимать величину 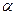постоянной.

г) Граничные условия четвертого рода характеризуют
условия теплообмена системы тел или тела с окружающей средой по
закону теплопроводности. Предполагается, что между телами осуществляется идеальный контакт (температуры, соприкасающихся поверхно­стей одинаковы).

В рассматриваемых условиях имеет место равенство тепловых по­токов, проходящих через поверхность соприкосновения:

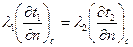(1.38)

В задачах с граничным условием четвертого рода задается отноше­ние тангенсов угла наклона касательных к температурным кривым в точке соприкосновения тел или тела и сре­ды (рисунок 1.4)

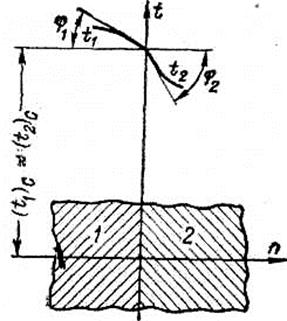
Рисунок 1.4 – К граничным условиям четвертого рода

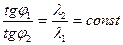(1.39)

Так как при совершенном контакте оба тела на поверхности соприкосновения имеют одинаковую температуру, то касательные у по­верхности раздела проходят через одну и ту же точку (рисунок 1.4).

Дифференциальное уравнение (1.26) со­вместно с условиями однозначности дают пол­ную математическую формулировку конкрет­ной задачи теплопроводности. Поставленная таким образом задача разрешается аналити­ческим, численным или экспериментальным

методом. В случае экспериментального решения задач теплопроводно­сти используются методы физического моделирования или тепловых аналогий.

Дата добавления: 2014-11-08