Дифференциальное уравнение теплопроводности

Лекция № 3

Тема: ОСНОВНЫЕ ПОЛОЖЕНИЯ УЧЕНИЯ О ТЕПЛОПРОВОДНОСТИ

План лекции

1.6 Дифференциальное уравнение теплопроводности

1.7 Условия однозначности для процессов теплопроводности

Изучение любого физического явления сводится к установлению за­висимости между величинами, характеризующими это явление. Для сложных физических процессов, в которых определяющие величины могут существенно изменяться в пространстве и времени, установить зависимость между этими величинами очень трудно. В этих случаях на помощь приходит метод математической физики, который исходит из того, что ограничивается промежуток времени и из всего пространства рассматривается лишь элементарный объем. Это позволяет в пределах элементарного объема и выбранного малого отрезка времени пренебречь изменением некоторых величин, характеризующих процесс, и сущест­венно упростить зависимость.

Выбранные таким образом элементарный объем d 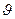и элементар­ный промежуток времени d , в пределах которых рассматривается изу­чаемый процесс, с математической точки зрения являются величинами бесконечно малыми, а с физической точки зрения — величинами еще достаточно большими, чтобы в их пределах можно было игнорировать дискретное строение среды и рассматривать ее как континуум (сплош­ную). Полученная таким образом зависимость является общим дифференциальным уравнением рассматриваемого процесса. Интегрируя диф­ференциальные уравнения, можно получить аналитическую зависимость между величинами для всей области интегрирования и всего рассматри­ваемого промежутка времени.

При решении задач, связанных с нахождением температурного по­ля, необходимо иметь дифференциальное уравнение тепло­проводности.

Для облегчения вывода этого дифференциального уравнения сде­лаем следующие допущения:

тело однородно и изотропно;

физические параметры постоянны;

деформация рассматриваемого объема, связанная с изменением температуры, является очень малой величиной по сравнению с самим объемом;

внутренние источники теплоты в теле, которые в общем случае мо­гут быть заданы как q_v=f(x, у, z, ), распределены равномерно.

В основу вывода дифференциального уравнения теплопроводности положен закон сохранения энергии, который в рассматриваемом случае может быть сформулирован следующим образом: количество теплоты dQ, введенное в элементарный объем извне за время d вследствие теп­лопроводности, а также от внутренних источников, равно изменению внутренней энергии или энтальпии вещества (в зависимости от рассмо­трения изохорического или изобарического процесса), содержащегося в элементарном объеме;

dQ₁ + dQ₂ =dQ, (1.22)

где dQ₁ — количество теплоты, Дж, введенное в элементарный объем путем теплопроводности за время d ; dQ₂— количество теплоты, кото­рое за время d выделилось в элементарном объеме d v за счет вну­тренних источников; dQ — изменение внутренней энергии или энтальпии вещества, содержащегося в элементарном объеме d v, за время d .

Для нахождения составляющих уравнения (1.22) выделим в теле эле­ментарный параллелепипед со сторо­нами dx, dy, dz (рисунок 1.3). Паралле­лепипед расположен так, чтобы его грани были параллельны соответству­ющим координатным плоскостям.

Количество теплоты, которое под­водится к граням элементарного объ­ема за время dx в направлении осей Ox, Оу, Oz, обозначим соответственно dQx, dQv, dQz.

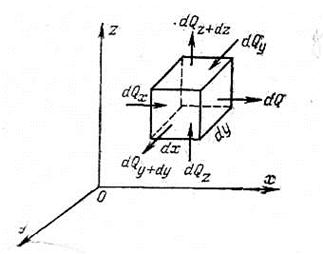
Рисунок 1.3- К выводу дифференциаль­ного уравнения теплопроводности.

Количество теплоты, которое бу­дет отводиться через противополож­ные грани в тех же направлениях, обозначим соответственно dQ_х+dх, dQ_y+dy, dQ_z+dz. Количество теплоты, подведенное к грани dy dz в на­правлении оси Ох за время d , составляет dO_x = q_xdy dz d , где q_x — проекция плотности теплового потока на направление нормали к ука­занной грани. Количество теплоты, отведенное через противоположную грань элементарного параллелепипеда в направлении оси Ох, запи­шется как

dQ_х+dх = q_x+dxdy dz d .

Разница количеств теплоты, подведенного к элементарному парал­лелепипеду и отведенного от него за время d в направлении оси Ох, представляет собой количество теплоты

dQ_х1=dQ_x-dQ_x+dx

или

dQ_x1 = q_xdy dz d —q_x+dxdy dz d (a)

Функция q_x+dx является непрерывной в рассматриваемом интервале dx и может быть разложена в ряд Тейлора:

q_x+dx=q_x+ …

Если ограничиться двумя первыми членами ряда, то уравнение (а) запишется в виде

dQ_x1= - 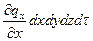(б)

Аналогичным образом можно найти количество теплоты, подводи­мое к элементарному объему и в направлениях двух других координат­ных осей Оу и Oz.

Количество теплоты dQ, подведенное теплопроводностью к рассма­триваемому объему, будет равно:

dQ₁= - 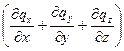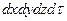(в)

Определим вторую составляющую уравнения (1.22). Обозначим ко­личество теплоты, выделяемое внутренними источниками в единице объема среды в единицу времени и называемое мощностью внутренних источников теплоты, через q_v, Вт/м³. Тогда

dQ₂ =q_vd v d (г)

Третья составляющая в уравнении (1.22) найдется в зависимости от характера термодинамического процесса изменения системы.

В случае рассмотрения изохорического процесса вся теплота, под­веденная к элементарному объему, уйдет на изменения внутренней энер­гии вещества, заключенного в этом объеме, т. е. dQ = dU.

Если рассматривать внутреннюю энергию единицы объема u = u(t, v), тогда dU найдется как

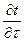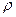
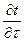dU = C _v d d v = c _v d d v (д)

где C_v — изохорная теплоемкость единицы объема, Дж/(м³-К); c_v — изохорная теплоемкость единицы массы, Дж/(кг-К); 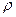— плотность ве­щества, кг/м³.

Подставляя полученные выражения (в), (г) и (д) в уравнение (1.22), получим:

с _v = - 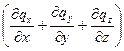+q _v (1.23)

или

с _v = - div q + q _v (1.23 ^/)

Выражение (1.23) является дифференциальным уравнением энер­гии для изохорического процесса переноса теплоты.

При рассмотрении изобарического процесса вся теплота, подведен­ная к объему, уйдет на изменения энтальпии вещества, заключенного в этом объеме, и уравнение (1.22) запишется следующим образом:

dQ₁ + dQ₂=dI. (1.24)

Если рассматривать энтальпию единицы объема, как i=i(t, p), то можно показать, что

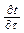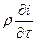dI=C_p d d v = с _p d d v= d d v (e)

где Ср — изобарная теплоемкость единицы объема, Дж/(м³-К); с_р — изобарная теплоемкость единицы массы, Дж/(кг-К).

Если полученные выражения (в), (г) и (е) подставить в уравне­ние (1.24), получим:

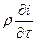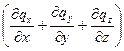= - +q _v (1.25)

или

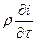= - div q + q _v (1.25')

Соотношение (1.25) является дифференциальным уравнением энер­гии в самом общем виде для изобарического процесса переноса тепло­ты. Уравнение (1.25) будет широко использоваться и в других разделах курса при рассмотрении конкретных видов переноса теплоты.

С учетом сказанного в общем виде уравнение запишется следующим образом:

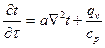(1.26)

Коэффициент пропорциональности а, м²/с, в уравнении (1.26) назы­вается коэффициентом температуропроводности и явля­ется физическим параметром вещества. Он существен для нестационар­ных тепловых процессов и характеризует скорость изменения темпера­туры. Если коэффициент теплопроводности характеризует способность тел проводить теплоту, то коэффициент температуропроводности являет­ся мерой теплоинерционных свойств тела. Из уравнения (1.26) следует, что изменение температуры во времени dt/d для любой точки прост­ранства пропорционально величине а. Иначе говоря, скорость измене­ния температуры в любой точке тела будет тем больше, чем больше коэффициент температуропроводности а. Поэтому при прочих равных условиях выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое обладает большим коэффи­циентом температуропроводности. Коэффициент температуропроводно­сти зависит от природы вещества. Например, жидкости >и газы обладают большой тепловой инерционностью и, следовательно, малым коэффи­циентом температуропроводности. Металлы обладают малой тепловой инерционностью, так как они имеют большой коэффициент температу­ропроводности. Далее, если система тел не содержит внутренних источ­ников тепла (q = 0), тогда выражение (1.26) принимает форму уравне­ния Фурье:

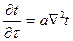(1.27)

Если имеются внутренние источники теплоты, но температурное поле соответствует стационарному состоянию, т. е. t = t(x, у, z), то диф­ференциальное уравнение теплопроводности превращается в уравнение Пуассона:

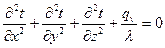(1.28)

Наконец, для стационарной теплопроводности и отсутствия внутрен­них источников теплоты выражение принимает вид уравнения Лапласа:

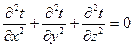(1.29)

Нахождение частных решений этих уравнений в частных производ­ных и некоторых других является основным содержанием теории тепло­проводности.

Дата добавления: 2014-11-08