Понятие векторного пространства

Лекция 2. Векторное пространство. Базис и координаты вектора

О п р е д е л е н и е. Векторным пространством над полем 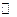действительных чисел называется множество элементов произвольной природы, для которых определены сложение и умножение на действительное число так, что выполняются аксиомы:

1. ;

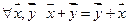2. ;

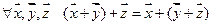3. ;

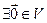
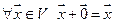4. .

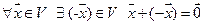5. ;

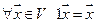6. ;

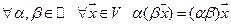7. ;

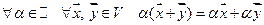8. .

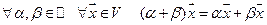При этом элементы множества называются векторами.

У п р а ж н е н и е.Доказать, что следующие множества являются примерами векторных пространств:

1. Множество всех свободных векторов геометрического пространства.

2. Множество всех свободных векторов геометрического пространства, параллельных данной плоскости.

3. Множество всех свободных векторов геометрического пространства, параллельных данной прямой.

4. Множество всех упорядоченных наборов из действительных чисел.

5. Множество всех многочленов от одной переменной, степень которых не превосходит .

Дата добавления: 2014-11-20