КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лабораторна робота № 5. Розв’язання системи лінійних рівнянь
|
|
|
|
Розв’язання системи лінійних рівнянь
Завдання 1. Розв’язати систему лінійних рівнянь методом Крамера
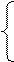x + 2y + z = 4
3x – 5y + 3z = 1
2x + 7y – z = 8
Рішення. Розв’язати систему лінійних рівнянь означає знайти таки значення невідомих X, Y, Z, що задовольняють кожному рівнянню системи.
Внесемо коефіцієнти системи в діапазон А2:С4, елементи вільного стовпчика – D2:D4. Згідно методу Крамера, розв’язок системи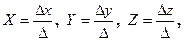 
де 
- відповідно головний та додаткові визначники системи. Скопіюємо коефіцієнти с заміною стовпчиків в діапазони А6:С8, А10:С12, А14:С16.
Розрахуємо головний визначник системи, використовуючи вбудовану математичну функцію МОПРЕД.
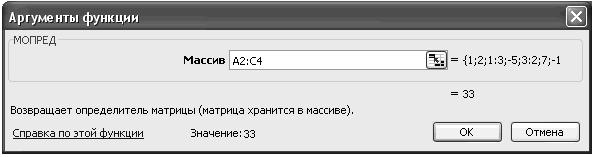
Інші визначники знайдемо аналогічно.
Тепер знайдемо корені системи за методом Крамера 
Зверніть увагу на використання абсолютних посилань в строчці формул.
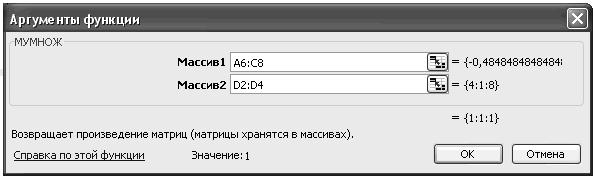
Тепер перевіримо правильність рішення. Так як в матричній формі система має вигляд 
, де А – матриця коефіцієнтів, 
- вектор-стовпчик невідомих, 
- вектор правої частини, то для перевірки достатньо матрицю А помножити на стовпчик (вбудована математична функція МУМНОЖ). Увага! Перед натисканням ОК утримати клавішу CTRL + SHIFT!
Отриманий вектор-стовбець (4,1,8) співпадає з вектором . Значить, розв’язок вірний.
Тепер розв’яжемо систему матричним методом.
Якщо в системі головний визначник не дорівнює нулю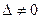 
, то для квадратної матриці А існує обернена матриця 
така, що 
, де Е – одинична матриця. Тоді рішення системи може бути знайдено за формулою 
.
Розрахуємо елементи оберненої матриці за допомогою вбудованої математичної функції МОБР.
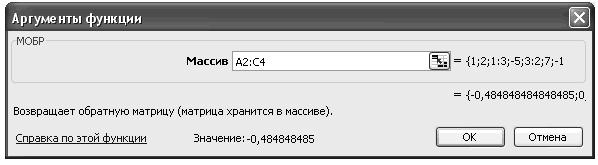
Увага! Перед натисканням ОК утримувати клавіші CTRL + SHIFT!
|
|
|
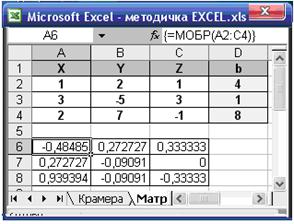
Знайдемо корені системи за формулою .
Увага! Перед натисканням ОК утримувати клавіші CTRL + SHIFT!
Очевидно, корені X, Y, Z, знайдені матричним методом, співпадають з результатом, отриманим за методом Крамера.
Варіанти для самостійної роботи
Завдання. Вирішити систему лінійних рівнянь методом Крамера та матричним методом.
Варіант №1. 
Варіант №2. 
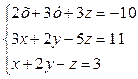
Варіант №3. 
Варіант №4. 
Варіант №5.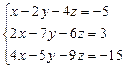 
Варіант №6.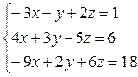 
Варіант №7. 
Варіант №8. 
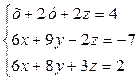
Варіант №9.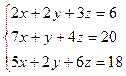 
Варіант №10.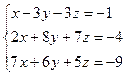 
Варіант №11.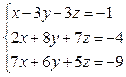 
Варіант №12. 
Варіант №13. 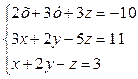Варіант №14. 
Варіант №15. 
Варіант №16.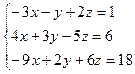 
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 600; Нарушение авторских прав?; Мы поможем в написании вашей работы!