Завдання. 1. За даними таблиці побудувати точковий графік

1. За даними таблиці побудувати точковий графік.

2. Знайти параметри лінійної залежності (а₀, а₁) за формуламиКрамера.

3. Знайти параметри лінійної залежності , використовуючи вбудовані статистичні функції «НАКЛОН» та «ОТРЕЗОК».

4. Для кожного табличного значення х_i отримати розрахункове значення y_i за формулою .

5. Побудувати графік табличних та розрахункових значень функції.

6. Використовуючи вбудовану в Excel статистичну функцію «ТЕНДЕНЦИЯ», створити прогноз для послідуючих, позатабличних значень аргументу х.

7. Отримати графічний прогноз, додавши на графіку лінію тренду.

8. В документі Microsoft Word створити звіт про роботу. У звіт внести основні розрахункові формули (використовувати об’єкт Microsoft Equation 3.0), графіки та скріншоти обчислень у Excel.

Варіанти завдань

Варіант №1.

X	1,79	2,74	4,05	4,87	6,12	8,07	9,01
Y	6,11	8,25	7,89	9,36	11,60	11,90	13,78

Варіант №2.

X	1,13	2,15	4,05	5,00	6,12	8,43	9,94
Y	6,11	8,25	7,89	10,13	12,00	11,90	14,72

Варіант №3.

X	1,13	2,15	4,05	5,00	6,12	8,43	9,64
Y	7,74	9,70	9,02	10,64	12,60	12,51	15,20

Варіант №4.

X	1,93	3,02	4,42	5,43	6,92	8,72	9,64
Y	7,74	10,47	9,70	11,49	14,40	14,50	17,33

Варіант №5.

X	1,31	2,14	5,12	6,66	8,54	10,40	13,08
Y	8,30	10,47	11,00	12,60	15,10	14,50	17,33

Варіант №6.

X	1,81	3,83	5,12	6,66	7,94	10,13	11,55
Y	8,80	9,50	12,30	11,90	15,10	15,40	18,50

Варіант №7.

X	2,85	4,32	5,58	7,72	8,92	10,95	12,10
Y	8,10	10,00	12,40	12,60	15,10	15,10	17,30

Варіант №8.

X	2,24	4,22	6,24	7,66	9,20	11,28	12,70
Y	3,35	7,09	8,00	10,15	12,60	13,70	16,00

Варіант №9.

X	1,97	4,22	5,55	7,86	8,85	11,28	12,42
Y	5,46	6,32	9,67	10,15	12,60	13,20	16,11

Варіант №10.

X	3,00	4,60	5,64	8,13	9,23	11,06	12,00
Y	5,46	7,76	10,00	11,11	13,60	14,40	16,66

Варіант №11.

X	1,53	3,34	5,75	7,50	8,59	11,11	13,14
Y	5,07	8,00	9,38	10,72	13,20	14,24	15,60

Варіант №12.

X	2,35	3,94	6,24	7,88	8,76	11,61	13,14
Y	5,07	8,00	9,38	10,24	12,73	13,79	15,41

Варіант №13.

X	2,57	4,32	6,84	7,98	9,47	12,43	13,96
Y	7,66	10,53	10,40	11,68	13,60	13,79	15,41

Варіант №14.

X	3,72	5,20	7,88	9,31	11,11	13,65	14,96
Y	7,56	10,53	10,63	12,80	14,65	15,03	16,80

Варіант №15.

X	3,72	5,84	9,12	10,36	11,82	14,74	16,72
Y	4,60	8,20	9,63	11,80	13,65	15,10	18,30

Варіант №16.

X	2,55	4,74	7,52	9,34	11,24	14,38	15,77
Y	5,70	7,80	8,30	10,34	12,93	14,10	15,50

Варіант №17.

X	2,19	4,45	7,15	9,20	11,39	15,62	17,37
Y	3,06	5,96	6,70	8,34	9,83	10,72	12,80

Варіант №18.

X	1,97	3,67	6,90	8,35	9,69	12,00	13,58
Y	3,06	5,20	6,70	8,54	9,73	10,12	13,20

Варіант №19.

X	1,89	3,56	5,54	6,89	7,65	8,79	9,45
Y	2,32	5,65	8,00	10,55	12,46	13,78	15,20

Варіант №20.

X	1,54	2,89	4,87	5,21	7,44	8,32	10,11
Y	2,33	5,57	7,00	9,05	10,47	13,53	14,23

6.2. Побудова рівняння квадратичної регресії

Мета роботи: Використати метод найменших квадратів для побудови рівняння квадратичної регресії, а також вбудовані математичні та статистичні функції Excel.

Отже, нехай в результаті експерименту отримана наступна таблиця залежності результативної ознаки Y від факторної ознаки:

X	X1	X2		Xn
Y	Y1	Y2		Yn

Побудувати аналітичну функцію , яка найкращім чином описує табличну.

Нехай точковий графік, що побудований за даними таблиці, має вигляд

Візуально визначаємо: точки розташовані по параболі, значить залежність квадратична: 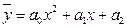. Параметри 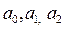треба визначити.

Критерій оптимальності за методом найменших квадратів

Середньоквадратичне відхилення

Умова мінімуму має вигляд

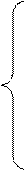
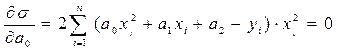
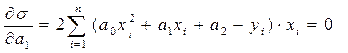
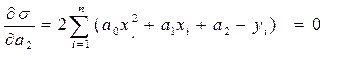
Після декількох алгебраїчних перетворень система буде мати наступний вигляд:

Це система трьох лінійних рівнянь з трьома невідомими .

Розв’яжемо систему матричним методом. З курсу вищої математики відомо, що у матричній формі система має вигляд 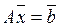, де А – матриця коефіцієнтів, – вектор-стовпчик невідомих, 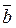- права частина. Тоді якщо 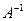- обернена матриця, така що 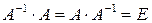, де - одинична матриця, то рішення системи має вигляд .

У нашому випадку рішенням системи будуть значення параметрів квадратичної залежності 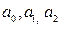. Покажемо по кроках увесь процес на конкретному прикладі.

Нехай результати вимірювань представлені таблицею.

X	1,25	2,54	3,74	4,87	6,12	7,78	8,55
Y	14,51	11,2	8,35	6,12	7,32	11,9	15,6

Створимо систему для обчислення параметрів 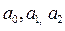та вирішимо ії матричним методом. Для обчислення елементів оберненої матриці будемо використовувати вбудовані функції Excel.

Спочатку обчислимо коефіцієнти системи

Отримані суми –це коефіцієнти системи. Створимо матрицю коефіцієнтів А и стовпчик b.

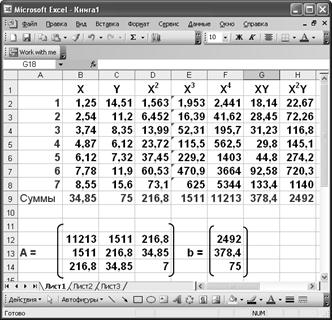
Для знаходження матриці 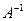, яка є оберненою даної , використаємо вбудовану математичну функцію МОБР.

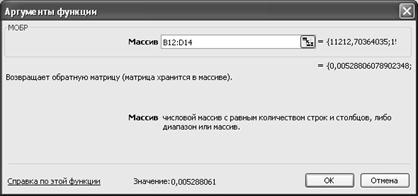
Увага!: при натисканні на кнопку ОК утримувати клавіші Ctrl+Shift.

Тепер обчислимо невідомі 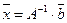, де 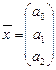- параметри рівняння регресії. Використаємо вбудовану математичну функцію МУМНОЖ (Увага!: при натисканні на кнопку ОК утримувати клавіші Ctrl+Shift).

Результати записані у стовпчику Х.

Отже, рівняння регресії має вигляд

.

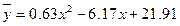Розрахуємо аналітичне значення функції та побудуємо лінію регресії.

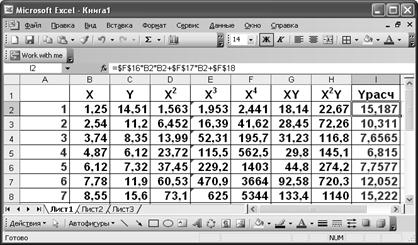
Побудуємо теоретичну криву.

Таким чином,, аналітична крива оптимально наближує (апроксимує) табличну.

Тепер, використовуючи аналітичну залежність, можна обчислити значення функції поза таблиці, а також побудувати прогноз на декілька кроків вперед.

Аналогічно лінійної залежності, можна побудувати графічний прогноз, додавши лінію тренду.

З урахуванням лінії тренду графік залежності має вигляд:

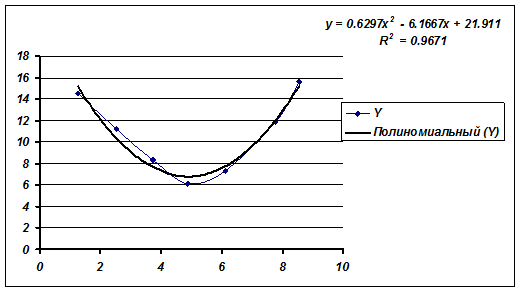
Варіанти завдань з теми «Аналіз та прогноз даних. Побудова рівняння квадратичної регресії»

Мета роботи: Вивчити метод найменших квадратів побудови рівняння регресії. Отримати навички використання вбудованих математичних та статистичних функцій для рішення практичних задач аналізу та прогнозу.

Дата добавления: 2014-11-08