Оценка качества модели регрессии

Построение модели множественной регрессии с выбранными факторами, экономический анализ коэффициентов уравнения

По результатам задания 1 получили трехфакторное уравнение регрессии вида

.

Экономический смысл коэффициентов уравнения: при увеличении ОС компании на 1 тысячу рублей ЧП будет уменьшаться на 38 рублей; при увеличении ПП на 1 тысячу рублей ЧП будет увеличиваться на 647 рублей; на каждую дополнительную тысячу КО прибыль будет расти на 72 рубля.

1) Проверка статистической значимости уравнения с помощью F-критерия Фишера

Расчетное значение F-критерия Фишера можно найти в регрессионном анализе (рисунок 7).

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		1.04794E+13	3.49313E+12	162.6049796	2.56059E-39
Остаток		2.25564E+12
Итого		1.2735E+13

Рисунок 7. Фрагмент трехфакторного регрессионного анализа

.

Так как 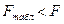, то уравнение трехфакторной регрессии статистически значимо на 95% уровне значимости. Таким образом, связь ЧП с включенными в модель факторами существенна.

2 ) Проверка предпосылки МНК о гомоскедастичности остатков

При проверке предпосылки МНК о гомоскедастичности остатков в модели множественной регрессии следует вначале определить, по отношению к какому из факторов дисперсия остатков более всего нарушена. Это можно сделать в результате визуального исследования графиков остатков, построенных по каждому из факторов, включенных в модель. Та из объясняющих переменных, от которой больше зависит дисперсия случайных возмущений, и будет упорядочена по возрастанию фактических значений при проверке теста Голдфельда-Квандта.

Для трехфакторной модели нашего примера графики остатков относительно каждого из трех факторов имеют вид, представленный на рисунке (эти графики легко получить в отчете, который формируется в результате использования инструмента Регрессия в пакете Анализ данных).

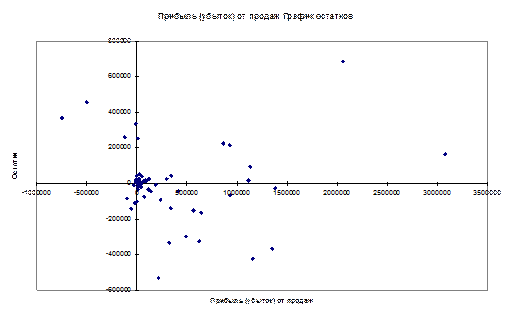
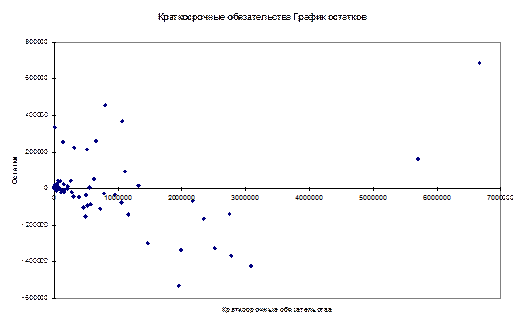
Рисунок 8. Графики остатков по каждому из факторов трехфакторной модели

На каждой из диаграмм ярко выражена направленность в распределении остатков, то есть непостоянство их дисперсии. В таком случае предпосылку о гомоскедастичности остатков следует проверять трижды, каждый раз упорядочивая значения переменных по возрастанию одного из факторов. Начнем с фактора, который имеет самое большое значение t-статистики, то есть с фактора ПП (t=10,282).

Основные этапы теста Голдфельда-Квандта:

1. Упорядочим переменные Y – ЧП, – ОС, – КО по возрастанию фактора 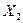– ПП (в Excel для этого можно использовать команду Данные – Сортировка – По возрастанию ).

2. Уберем из середины упорядоченной совокупности С=1/4*n=1/4*109 27 значений. В результате получим две совокупности по ½*(109-27)=41 значению соответственно с малыми и большими значениями .

3. Для каждой совокупности в отдельности выполним регрессионный анализ (рисунок 9).

Для первой совокупности:

Дисперсионный анализ
	df	SS	MS
Регрессия
Остаток		2.04901E+11
Итого		2.27839E+11
	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	10965.13577	13026.38488	0.841763534
ОС	0.002340442	0.040854765	0.057286887
КО	-0.09932818	0.057414794	-1.730010202
ПП	-0.220959047	0.120684593	-1.830880326

Для второй совокупности:

Дисперсионный анализ
	df	SS	MS
Регрессия		9.15293E+12	3.05098E+12
Остаток		1.35495E+12
Итого		1.05079E+13
	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	-72702.62526	38053.26016	-1.910549187
ОС	-0.057544265	0.022085349	-2.60554026
КО	0.029880567	0.034694784	0.861240878
ПП	0.869087051	0.10222039	8.50209095

Рисунок 9. Фрагменты регрессионного анализа для первой и второй совокупностей соответственно

4. Найдем отношение полученных остаточных сумм квадратов (в числителе должна быть большая сумма):

R=1.35495Е+12/2,04901Е+11=

6,612694

5. Вывод о наличии гомоскедастичности остатков делаем с помощью F-критерия Фишера с уровнем значимости 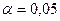и двумя одинаковыми степенями свободы 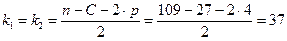(здесь р – число параметров (коэффициентов) в уравнении регрессии):

.

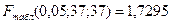Так как 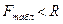, то обнаруживается наличие гетероскедастичности в остатках модели по отношению к фактору .

Аналогично обнаруживается наличие гетероскедастичности в остатках при упорядочении значений переменных по каждому из двух оставшихся факторов и . Эти процедуры проводятся в полном соответствии с рассмотренной процедурой. Мы их опускаем.

Дата добавления: 2014-11-20