Тема 1 5. Законы идеальных газов

15.1 Макроскопические состояния

Число молей вещества: ν = m/M; ν = V/V_M, где m – масса; M - молярная масса; V – объем, V_M – молярный объем.

Масса одной молекулы: m₀= M/N_A; m₀ = ρ/n, где М – молярная масса, N_A = 6,023·10²³ моль^-1 - число Авогадро; ρ - плотность; n₀ - концентрация, определяется из соотношений: n₀ = N/V; n = ρ/m₀; n = N_A/M.

Число молекул в данной массе вещества: N = m/m₀ = m N_a/M.

Термодинамическая температура связана с температурой шкалы Цельсия T ,K = t°C +273,15; t°C = T,K – 273,15°С

9.2 Уравнения состояния идеального газа. Изопроцессы

Уравнения состояния идеального газа (уравнение Менделеева –Клапейрона): для одного моля газа; pV_м = RT - для произвольной массы газа: pV = mRT/M; pV = νRT - где V_м - молярный объем; M - молярная масса; m – масса газа; ν = m/M -количество вещества; R – универсальная газовая постоянная

Объединенный газовый закон (уравнение Клапейрона): pV/T =const; p₁V₁/T₁ = p₂V₂/T₂ где p –давление газа; V –объем; T – термодинамическая температура

Закон Бойля –Мариотта (изотермический процесс): pV = const; p₁V₁= p₂V₂ при T=const, m = const

Закон Гей-Люссака (изобарический процесс): V =V₀(1 + αt) или V/T =const; V₁/V₂= T₁/T ₂ при p =const, m =const Закон Шарля (изохорический процесс): р= р₀(1 + αt) или p/T =const; p₁/p₂ = T₁/T₂ при V =const, m =const, где t –температура по шкале Цельсия, V₀, p₀ –соответственно объем и давление при 0⁰С, коэффициент α =1/273 К^-1, p, V, T соответственно давление, объем и термодинамическая температура

Закон Дальтона для давления смеси n идеальных газов: p = 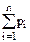, где p_i - парциальное давление i -ой компоненты газа

Закон Авогадро: при Т₀ = 0⁰С =273 К, р₀ =1 атм =1,013·10⁵ Па мольный объем любого газа V_м =22,4 л ·моль^-1 = 2,24·10^-2 м³·моль^-1

Пример 20. В двух баллонах имеются два газа: водород – Н₂ и углекислый газ – СО₂. Во сколько раз число молекул одного газа больше числа молекул другого газа, если массы газов одинаковы?

Условие:

М₁ =2·10^-3 кг/моль;

М₂ =44·10^-3 кг/моль;

N₁/N₂ -?

Решение. В одном моле вещества содержится число молекул, равное числу Авогадро N =6,02·10²³ моль^-1. Количество вещества водорода ν = m/M_1, а в углекислом газе содержиттся число молей ν₂ = m/M₂. Тогда число молекул водорода N₁ = ν₁N_A = mN_A/M₁, число молекул углекислого газа N₂ = ν₂N_A = mN_A/M₂.

Разделив N₁ на N₂, получим ответ

N₁/N₂ = M₂/M₁ = 44/2 = 22

Пример 21. В баллоне объемом V = 10 л находится гелий под давлением р₁ = 1 МПа и при температуре Т₁ = 300 К. После того, как из баллона было взято m = 10 г гелия, температура в баллоне понизилась до Т₂ = 290 К. Определить давление р₂ гелия, оставшегося в баллоне, и изменение внутренней энергии газа.

Условие:

V = 10 л = 10^{-2 м3};

р₁ = 1,0 МПа = 1,0·10⁶ Па;

Т₁ = 300 К;

m = 10 г = 1,0·10^{-2 кг;}

Т₂ = 290 К;

R = 8,314 Дж/кг·К;

М = 4·10^-3 кг/моль;

р₂ -? U -?

Решение. Воспользуемся уравнением Менделеева-Клапейрона, применив его к конечному состоянию газа:

р₂V = m₂RT₂/M, (1)

где m₂ – масса гелия в конечном состоянии;

М – молярная масса гелия;

R – универсальная газовая постоянная.

Из уравнения (1) выразим искомое давление

р₂ = m₂RT₂/MV. (2)

Массу m₂ гелия выразим через массу m₁, соответствующую начальному состоянию, и массу m гелия, взятого из баллона:

m₂ = m₁ – m. (3)

Массу m₁ гелия найдем также из уравнения Менделеева- Клапейрона, применив его к начальному состоянию:

m₁ = Mp₁V/RT₁. (4)

Подставив выражение массы m₁ в уравнение (2), а затем выражение m₂ в уравнение (1), найдем

p₂ = (Mp₁V/RT₁ – m)RT₂/MV, (5)

.

Формула (5) дает единицу давления

[p] = К·Па/К – кг · Дж · К · моль/(кг · моль · м³·К) =

= Па – Дж/м³ = Па – Н·м/м³ = Па.

Вычисления

р₂=290·10⁶/300 – 1,0·10^-2·8,314·290/(4·10^-3·10^-2) = 3,64·10⁵ Па.

Внутренняя энергия газа в исходном состоянии

U₁ = m₁iRT₁/2M.

Для газа, оставшегося в баллоне

U₂ = m₂ iRT₂/2M.

Изменение энергии газа

U = U₁ – U₂ = R(m₁ – m₂) (T₁ – T₂)/M = Rm (T₁ – T₂)/M.

Проверка размерности: [U] = Дж·кг·К·моль/моль·К·кг = Дж.

Ответ: U = 208 Дж.

ЗАДАНИЕ 16. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНОГО ГАЗА

16.1 Идеальный газ как модельная термодинамическая система. Статистические распределения

Основное уравнение молекулярно-кинетической теории газов: p = n₀m<v²_кв>/3; p = ρ<v²_кв>/3; p =2n<ε>/3; <ε> = m<v_кв²>/2, где <v_кв > -средняя квадратичная скорость молекул; <ε> - средняя кинетическая энергия поступательного движения молекулы; n₀ –концентрация молекул; m - масса одной молекулы; ρ - плотность газа

Закон Максвелла для распределения молекул идеального газа по скоростям: f(v) = dN(v)/Ndv = 4π (m₀/2πkT)^3/2v²exp [ - m₀v²/2kT], где функция f(v) распределения молекул по скоростям определяет число молекул dN(v)/N из общего числа молекул, скорости которых лежат в интервале от v до v+dv

Барометрическая формула: p = p₀ exp [ - Mg (h – h₀)/RT]; p = p₀exp[ - m₀g(h – h₀)/kT], где р и р₀ – давление газа на высоте h u h₀, M - молярная масса газа, m₀ -масса молекулы, R - универсальная газовая постоянная, k - постоянная Больцмана Распределение Больцмана во внешнем центральном поле: n = n₀ exp [ -Mgh/RT]; n = n₀ exp [-m₀gh/kT]; n = n₀exp[- W_п/kT], где n, n₀ -концентрация молекул на высоте h и h₀=0; W_п - потенциальная энергия молекул в поле тяготения

Скорости молекул: наиболее вероятная: v_b = (2RT/M)^1/2 = (2kT/m₀)^1/2 = (2p/ρ)^1/2 средняя квадратичная: <v_кв> =(3RT/M)^1/2= (3kT/ m₀)^1/2 =(3p/ρ)^1/2 средняя арифмeтическая: <v> = (8RT/πM)^1/2 =(8kT/πm₀)^1/2= (8p/πρ)^1/2 где T - абсолютная температура газа; M - молярная масса газа; m₀ – масса одной молекулы; p - давление газа; ρ – плотность газа; R – универсальная газовая постоянная; k – постоянная Больцмана

Средняя кинетическая энергия поступательного движения молекулы: <ε_k> =3kT/2. Средняя полная энергия молекулы: <ε_k> = ikT/2, где i- число степеней свободы молекул; k – постоянная Больцмана; T –термодинамическая температура одноатомный газ: i =3; двухатомный газ: i=5; многоатомный газ: i =6.

Зависимость давления газа от температуры: p = nkT

Пример 22. Температура окиси азота NO Т =300 К. Определить долю молекул, скорости которых лежат в интервале от v₁ = 820 м/с до v₂ = 830 м/с

Условие: Т = 300 К; v1 = 820 м/с; v2 = -830 м/c; ∆N /N -?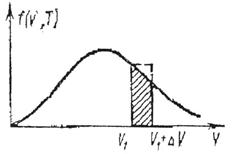

Решение. Рассматриваемый газ находится в равновесном состоянии, и согласно Максвеллу, относительное число молекул, скорость которых заключена в интервале от v до v + dv

ΔN/N = f (v, T)dv,

где f (v, T) – функция Максвелла;

dv – настолько малый диапазон скоростей, что в пределах его заведомо f (v, T) = const.

В условии задачи требуется определить долю молекул, скорости которых лежат в диапозоне ∆v = v₂ – v₁ = 10 м/с.

Если в этом пределе функцию Максвелла можно считать с достаточной точностью постоянной, то искомая величина может быть рассчитана по приближенной формуле

∆N/N = f (v₁, N)∆v. (1)

Такое приближение соответствует тому, что на рис. 6 заштрихованная площадь приравнивается к площади прямоугольника с основанием v₁ и высотой, равной значению f (v, T).

Следовательно, прежде всего надо найти значения функции Максвелла при v = v₁ и v = v₂ и выяснить, какую погрешность может дать использование равенства (1).

Функция Максвелла имеет вид

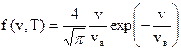, (2)

где v_в = (2kT/m₀)^1/2 = (2RT/M)^1/2 - (3)

- наиболее вероятная скорость молекул

Для облегчения расчета найдем сначала наиболее вероятную скорость по равенству (3) v_b = 410 м/с.

Тогда согласно (2)

f(v₁,T) = 4,03·10^-4 c/м f(v₂, T) = 3,75·10^-4 c/м.

Это означает, что при использовании выражения (23) допускается ошибка относительная величина которой

δf = [f(v₁, T) – f (v₂, T)]/f (v₁, T) = 0,07 = 7%.

Следовательно, с указанной степенью точности можно использовать равенство (2). Тогда доля молекул, скорости которых лежат в заданном интервале

ΔN/N = f (v₁, T)∆v = 4,0 ∙ 10^-3 = 0,4%.

Дата добавления: 2014-11-20