Независимые события. Примеры. Теорема умножения вероятностей

Несовместимые события. Примеры. Теорема сложения вероятностей.

Несовместимыми называются события, которые вместе не наступают. Например, одновременное выпадение на одном игральном кубике и 1 и 2, или при подбрасывании монеты одновременное выпадение и орла и решки, или одновременное нахождение одного человека в Петербурге и в Москве.

Теорема сложения вероятностей: вероятность появления одного (безразлично какого) события из нескольких несовместных событий равна сумме их вероятностей.

Для двух несовместных событий

Р(А или В) = Р(А) +Р(В)

Доказательство:

Пусть n – общее число испытаний, m₁ – число случаев, благоприятствующих событию А, m₂ – число случаев, благоприятствующих событию В. Число случаев, благоприятствующих наступлению либо события А, либо события В, равно m₁ + m₂. Тогда

Р(А или В) = (m₁ + m₂)/n = m₁/n +m₂/n.

Отсюда, учитывая, что P(A)=m/n, имеем:

Р(А или В) =Р(А) +Р(В)

1. В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если значение одной из них не влияет на вероятность значений другой.

Пример 1. Пусть брошены три уравновешенные монеты. Определим события следующим образом:

§ : монеты 1 и 2 упали одной и той же стороной;

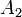§ : монеты 2 и 3 упали одной и той же стороной;

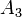§ : монеты 1 и 3 упали одной и той же стороной;

Легко проверить, что любые два события из этого набора независимы. Все же три в совокупности зависимы, ибо зная, например, что события произошли, мы знаем точно, что 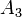также произошло.

Теорема умножения вероятностей: вероятность совместного поведения независимых событий равна произведению их вероятностей.для 2 событий P(A и B)= Р(А)* Р(В)

Дата добавления: 2014-11-20