
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методические указания 1 страница
|
|
|
|
Тема 6. Индексы
1. Понятие индексов.
2. Индивидуальные индексы и их свойства.
3. Агрегатные формы общего индекса.
4. Взаимосвязь общих индексов и условия ее осуществления.
5. Средняя арифметическая и гармоническая формы общих индексов.
6. Индексы качественных показателей или средних уровней.
Индексы – одни из наиболее распространенных обобщающих показателей в статистике. Очень важно усвоить понятие индекса (в широком и узком смысле), классификацию индексов, классификацию показателей при построении индексов, основные обозначения (символы) в этой теме.
В широком смысле индексами в статистике называют относительные величины, характеризующие изменение уровня явления во времени, результат сопоставления изучаемого явления в пространстве, а также уровень планового задания и степень выполнения плана.
В узком смысле индексами (собственно индексами) называют обобщающий показатель сравнения двух совокупностей, состоящих из элементов, непосредственно не поддающихся суммированию. Такие индексы строятся для сложных явлений – неоднородных совокупностей.
В зависимости от характера совокупности различают индивидуальные и общие индексы; по форме построения различают агрегатные и средние взвешенные (арифметические и гармонические) индексы; по применяемым весам – индексы с постоянными весами и переменными весами; по составу явления – индексы переменного состава, постоянного состава, а также индекс структурных сдвигов;
При построении индексов используют классификацию показателей на факторные (количественные и качественные) и результативные.
Факторные показатели выступают в качестве аргумента, влияющего на изменение сложного показателя. Результативные показатели выступают в качестве функции, изменяются под влиянием факторных показателей.
Количественные показатели характеризуют объем какого-либо явления по совокупности или ее части, например:
q – физический объем товарооборота (количество проданных товаров в натуральном выражении). Этим же символом обозначают физический объем продукции (количество произведенной продукции).
К количественным показателям относят также посевную площадь, численность работников (рабочих) и др.
Качественные показатели характеризуют уровень явления, т.е. рассчитываются на единицу совокупности. К этой группе показателей относятся:
p – цена единицы товара (продукции, работ, услуг),
z – себестоимость единицы продукции, работ, услуг,
t – трудоемкость единицы продукции (затраты рабочего времени на производство единицы продукции),
w – производительность труда (выработка продукции в единицу времени или на одного работающего) и другие показатели.
Результативные (или сложные, производные, количественно-качественные) показатели отражают результат взаимодействия количественно-качественных показателей. К этой группе относятся следующие показатели:
S – товарооборот (стоимость проданных товаров, выручка, потребительские расходы населения). Этим же символом можно обозначить стоимость произведенной на предприятии продукции, S = pq,
T – затраты рабочего времени (труда) на производство продукции (выражаются в чел/часах, чел/днях), T = tq.
C – затраты на производство продукции (себестоимость произведенной продукции), С = z q, и другие показатели.
Основные вопросы в этой теме – индивидуальные и общие индексы. Различают базисные и цепные индивидуальные индексы. Усвоив различие экономического смысла этих индексов и задач, решаемых с их помощью, переходят к свойствам индивидуальных индексов и их значению. Индивидуальные индексы строятся для однородных (соизмеримых) совокупностей. Общие индексы строятся для неоднородных (несоизмеримых) совокупностей. Методология построения различных общих индексов (в агрегатной форме, в средних формах) и составляет главное содержание теории индексов и индексного метода анализа. Необходимо научиться строить формулы индексов важнейших экономических показателей: цен, физического объема товарооборота, товарооборота, себестоимости, затрат на производство, трудоемкости, производительности труда и др. При построении агрегатной формы индексов различных показателей пользуются соответствующими правилами взвешивания индексов. При построении средней арифметической и средней гармонической формы (формул) индексов обращают внимание на возможности их практического использования в экономико-статистическом анализе. Для характеристики изменения во времени средней величины качественного показателя (цены, себестоимости и др.) используют систему взаимосвязанных индексов: переменного состава (среднего уровня), постоянного состава и структурных сдвигов. Необходимо уяснить их экономический смысл, область применения каждого из трех индексов, а также взаимосвязь между ними.
В этой же теме необходимо обратить внимание на взаимосвязи общих индексов, условия их осуществления, на возможности индексного факторного анализа.
Для успешного усвоения темы 6 необходимо ознакомиться с представленным теоретическим материалом и целесообразно решить предлагаемые задачи.
Индивидуальный индекс (i) представляет собой отношение величины показателя в отчетном (текущем) периоде к его величине в базисном периоде. В общем виде этот индекс может быть записан в виде формулы:
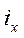 =
= 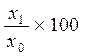 *,
*,
«0» и «1» обозначают соответственно базисный и отчетный периоды.
где x – индексируемый показатель (количественный, качественный, результативный),
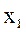 - величина показателя отчетного (текущего) периода (сравниваемый уровень),
- величина показателя отчетного (текущего) периода (сравниваемый уровень),
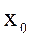 - величина показателя базисного периода (базисный уровень).
- величина показателя базисного периода (базисный уровень).
Общий индекс – это относительная величина, характеризующая результат сравнения непосредственно несоизмеримых явлений.
Общие индексы вычисляют для сложных совокупностей, состоящих из различных по натурально – вещественной форме единиц (например, для набора различных потребительских товаров). Общие индексы строят различно для количественных, качественных и результативных показателей.
В общих индексах различают два элемента: индексируемая величина – показатель, изменение которого характеризует индекс и веса - постоянный элемент. Основной исходной формой любого общего индекса является агрегатная форма.
Особенностью агрегатной формы общего индекса является то, что в нем непосредственно сравниваются две суммы одноименных показателей. Они представляют собой отношение сумм произведений индексируемых величин и весов. Так как весами служат показатели экономически тесно связанные с индексируемыми величинами, то полученные произведения образуют определенные экономические категории.
Агрегатная форма (формула) общего индекса цен теоретически строится, как правило, по двум схемам: Э. Ласпейреса и Г. Пааше, соответственно:
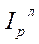 =
= 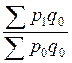 и
и 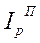 =
= 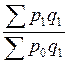 ,
,
где 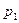 и
и 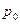 - индексируемый показатель (цена), который является переменным элементом (в числителе берется на отчетном уровне, а в знаменателе – на базисном уровне);
- индексируемый показатель (цена), который является переменным элементом (в числителе берется на отчетном уровне, а в знаменателе – на базисном уровне);
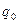 (или
(или 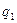 ) - веса - постоянный элемент, т.е. в числителе и знаменателе физический объем товарооборота, базисного или отчетного периода, что позволяет устранить влияние изменения этого показателя.
) - веса - постоянный элемент, т.е. в числителе и знаменателе физический объем товарооборота, базисного или отчетного периода, что позволяет устранить влияние изменения этого показателя.
Знак 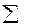 означает, что суммируются стоимости (
означает, что суммируются стоимости (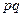 ) различных товаров. Количество слагаемых зависит от количества видов товаров.
) различных товаров. Количество слагаемых зависит от количества видов товаров.
Общий индекс цен (по любой схеме и в любой форме) показывает изменение цен в среднем по совокупности товаров в отчетном периоде по сравнению с базисным, или изменение потребительских расходов населения в отчетном периоде по сравнению с базисным при неизменных показателях уровня и структуры потребления.
Из двух схем общего индекса цен предпочтение, в условиях рыночной экономики, роста потребительских цен и изменения уровня и структуры потребления, отдается схеме Э. Ласпейреса. На основе этой схемы строится в РФ индекс потребительских цен – один из важнейших макроэкономических показателей, по величине которого судят, в частности, об уровне инфляции в стране.
На основе общего индекса цен в агрегатной форме определяется экономия (потери) населения (в д.е.). Экономия определяется как разность между числителем и знаменателем индекса, т.е.
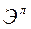 =
= 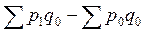 - условная экономия
- условная экономия
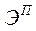 =
= 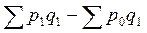 - фактическая экономия
- фактическая экономия
Если эта разность (в денежных единицах) имеет знак «-» это означает экономию, если «+», то потери населения (в результате роста цен). Заметим, что в факторном индексном анализе эту же разность называют абсолютным приростом (снижением) товарооборота в результате изменения цен (т.е. влияния одного этого фактора).
Агрегатная форма (формула) общего индекса себестоимости строится следующим образом:
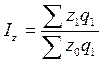
Агрегатная форма (формула) общего индекса трудоемкости строится следующим образом:
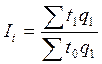 ,
,
где t – трудоемкость единицы продукции,
q – количество произведенной продукции в натуральном выражении,
Индексы трудоемкости показывают относительное изменение трудоемкости по одному виду продукции, или в среднем по нескольким видам продукции.
Общий индекс производительности труда рассчитывается только на основе обратного показателя – трудоемкости (t):
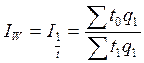 ,
,
где 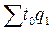 - общие затраты рабочего времени на продукцию, произведенную в отчетном периоде по трудоемкости базисного периода.
- общие затраты рабочего времени на продукцию, произведенную в отчетном периоде по трудоемкости базисного периода.
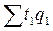 - общие затраты рабочего времени на продукцию отчетного периода по трудоемкости отчетного периода.
- общие затраты рабочего времени на продукцию отчетного периода по трудоемкости отчетного периода.
Разность между знаменателем и числителем называют экономией (-) или дополнительными затратами (+) рабочего времени вследствие изменения трудоемкости (производительности труда), которая выражается в чел/днях. Индексы производительности труда показывают относительное изменение производительности труда по какому-либо виду продукции или в среднем по совокупности нескольких видов продукции.
Общие индексы качественных показателей в агрегатной форме взвешиваются по весам отчетного периода. Это правило относится ко всем индексам качественных показателей, кроме индекса цен, который может быть взвешен по весам как отчетного, так и базисного периодов. Как было отмечено выше, предпочтение в большинстве стран с рыночной экономикой отдается общему индексу цен, взвешенному по весам базисного периода.
Агрегатная форма общего индекса физического объема товарооборота. Теоретически этот индекс может быть построен также по двум схемам:
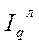 =
= 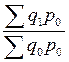 и
и 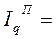
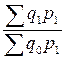 .
.
В этих индексах индексируемой (переменной) величиной является количество товара (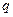 ), весами (постоянной величиной) – цены базисного (
), весами (постоянной величиной) – цены базисного (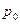 ) или отчетного (
) или отчетного (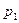 ) периода. На практике чаще используется первая схема, в которой взвешивание производится по весам базисного периода. Оба индекса показывают изменение количества проданных товаров в среднем по какой-либо их совокупности. Если, например,
) периода. На практике чаще используется первая схема, в которой взвешивание производится по весам базисного периода. Оба индекса показывают изменение количества проданных товаров в среднем по какой-либо их совокупности. Если, например, 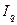 = 2 или 200%, то это означает увеличение количества в среднем в 2 раза, или на 100%.
= 2 или 200%, то это означает увеличение количества в среднем в 2 раза, или на 100%.
Заметим, что в факторном индексном анализе разность между числителем и знаменателем общего индекса физического объема товарооборота, например, 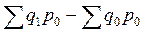 , называют абсолютным приростом товарооборота за счет изменения количества проданных товаров (в денежных единицах).
, называют абсолютным приростом товарооборота за счет изменения количества проданных товаров (в денежных единицах).
Агрегатная форма общего индекса количества произведенной продукции.
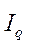 =
= 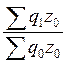
Общие индексы количественных показателей в агрегатной форме взвешиваются по весам базисного периода.
Агрегатная форма общего индекса товарооборота (стоимости реализованных товаров). В отличие от предыдущих индексов (качественного, затем количественного показателя), индекс названного – количественно-качественного показателя (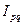 ) строится проще – как отношение сумм соответствующего показателя отчетного и базисного периода, т.е.
) строится проще – как отношение сумм соответствующего показателя отчетного и базисного периода, т.е.
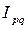 =
= 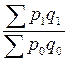 ,
,
где 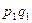 - товарооборот отчетного периода по совокупности каких-либо товаров,
- товарооборот отчетного периода по совокупности каких-либо товаров,
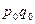 - товарооборот базисного периода по той же совокупности.
- товарооборот базисного периода по той же совокупности.
Общий индекс товарооборота показывает изменение товарооборота в среднем по какой-либо совокупности товаров в отчетном периоде по сравнению с базисным периодом.
Заметим, что в факторном индексном анализе разность между числителем и знаменателем рассмотренного индекса называют абсолютным приростом товарооборота за счет влияния двух факторов, т.е. изменения цен и количества проданных товаров.
Агрегатная форма общего индекса затрат на продукцию:
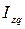 =
= 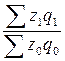
Агрегатная форма общего индекса затрат рабочего времени на производство продукции:
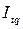 =
= 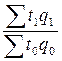
Общие индексы результативных показателей в агрегатной форме строятся как отношение сумм соответствующих показателей двух периодов и взвешивания не требуют.
На практике часто имеются данные не за два, а за несколько последовательных периодов времени. В таких случаях строится система общих индексов, состоящая из ряда индексов, характеризующих последовательное изменение изучаемого явления во времени, что обеспечивает их сопоставимость.
Различают 4 способа построения такой системы:
1) система цепных индексов с постоянными весами
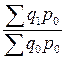 …
… 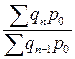 .
.
2) система цепных индексов с переменными весами
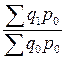 …
… 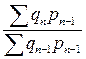 .
.
3) система базисных индексов с постоянными весами
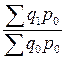 …
… 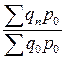 .
.
4) система базисных индексов с переменными весами
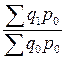 …
… 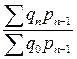 .
.
Ранее была установлена взаимосвязь индивидуальных индексов товарооборота (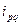 ), цен (
), цен (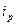 ) и физического объема товарооборота (
) и физического объема товарооборота (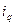 ):
):
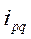 =
= 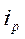
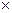
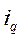 .
.
Между общими индексами этих показателей существует аналогичная взаимосвязь:
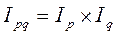 .
.
Подставим в данное уравнение агрегатную формулу каждого индекса:
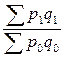 =
= 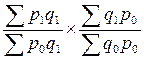 .
.
Таким образом, взаимосвязь имеет место.
Очевидно, взаимосвязь имеет место при условии, что индексы сомножители взвешиваются по весам разных периодов (один по весам отчетного периода, а другой по весам базисного периода, или наоборот). Если это условие не выполняется, взаимосвязь теряет силу.
Взаимосвязь общих индексов позволяет вычислить любой из трех взаимосвязанных индексов, если известны два других. С помощью взаимосвязи общих индексов изучают роль отдельных факторов в изменении сложных (результативных) показателей.
Заметим, что общие индексы цен, себестоимости, трудоемкости и производительности труда из агрегатной формы могут быть преобразованы в средние формы. Средние формы общего индекса, являются производными от агрегатной формы. Существуют 2 средние формы общих индексов средняя арифметическая и средняя гармоническая.
Преобразование агрегатного индекса в средний арифметический осуществляется путем подстановки в числитель агрегатного индекса вместо индексируемой величины ее выражения через индивидуальный индекс, т.е.
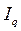 =
= 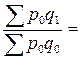
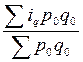 ,
,
где 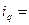
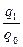
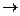
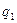 =
= 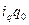 .
.
Из формулы видно, что этот индекс представляет собой специфически взвешенную среднюю арифметическую из индивидуальных индексов (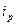 ). Роль весов выполняет товарооборот базисного периода в фактических ценах (
). Роль весов выполняет товарооборот базисного периода в фактических ценах (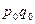 ).
).
Записанная средняя арифметическая формула общего индекса цен более удобна для практического применения, по сравнению с агрегатной, которая требует расчета товарооборота базисного периода в ценах отчетного периода (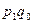 ).
).
По изложенной схеме можно любой агрегатный индекс аналогично преобразовать в средний арифметический.
Преобразование агрегатного индекса в средний гармонический осуществляется путем подставки в знаменатель индекса вместо индексируемой величины ее выражения через индивидуальный индекс, т.е.
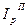 =
= 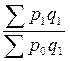 =
= 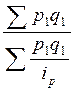
где 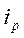 =
= 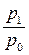
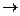
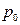 =
= 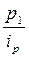 .
.
Полученная форма индекса представляет собой специфически взвешенную среднюю гармоническую из индивидуальных индексов (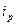 ). Роль весов выполняет товарооборот отчетного периода (
). Роль весов выполняет товарооборот отчетного периода (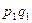 ).
).
Аналогично преобразовываются другие агрегатные индексы в средние гармонические.
Необходимо заметить, что по экономическому смыслу и средний арифметический и средний гармонический индекс будут тождественны агрегатному индексу.
Необходимость в применении индексов переменного и постоянного состава и индекса структурных сдвигов возникает в том случае, когда динамика средних показателей отражает не только изменение осредняемого признака, но и изменение состава данной совокупности.
Индекс переменного состава называют еще индексом среднего уровня, так как он показывает изменение средней величины явления, например, изменение средней цены 1 кг мяса по совокупности рынков; или средней себестоимости 1 кг хлебобулочных изделий по совокупности хлебозаводов и т.п.
В общем виде индекс переменного состава - это отношение средней величины качественного показателя в отчетном периоде к средней его величине в базисном периоде. Индекс может быть записан в двух вариантах, в зависимости от характера весов:
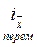 =
= 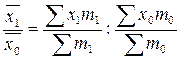 или
или 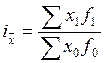 ,
,
где 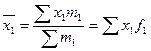 - средняя величина (средняя арифметическая взвешенная) показателя в отчетном периоде,
- средняя величина (средняя арифметическая взвешенная) показателя в отчетном периоде,
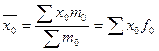 - то же в базисном периоде,
- то же в базисном периоде,
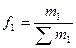 и
и 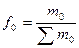 - доли отдельных частей совокупности в ее общем объеме соответственно в отчетном и базисном периодах.
- доли отдельных частей совокупности в ее общем объеме соответственно в отчетном и базисном периодах.
По первому варианту в формуле используются веса – m - абсолютные показатели, по второму варианту – f - относительные показатели (доли, удельные веса).
Заметим, что разность между числителем и знаменателем каждого индекса, в частности 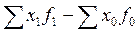 , показывает абсолютное изменение средней величины изучаемого показателя за счет совместного влияния двух факторов.
, показывает абсолютное изменение средней величины изучаемого показателя за счет совместного влияния двух факторов.
Индекс переменного состава показывает изменение средней величины показателя (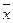 ) за счет совместного влияния двух факторов:
) за счет совместного влияния двух факторов:
1) изменения уровня индексируемого показателя в отдельных частях совокупности (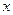 ),
),
2) изменения частей совокупности (m) или доли (удельного веса) этих частей совокупности (f), т.е. изменения структуры совокупности, структурных сдвигов.
Следовательно, для того, чтобы охарактеризовать изменение средней величины показателя за счет каждого фактора в отдельности, нужно поочередно устранить (элиминировать) влияние одного из факторов, зафиксировав его на постоянном уровне.
Эта задача решается с помощью индексов постоянного состава и структурных сдвигов.
Влияние изменения уровня индексируемого показателя в отдельных частях совокупности (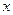 ) оценивается с помощью индекса постоянного состава
) оценивается с помощью индекса постоянного состава
Индекс постоянного состава может быть записан в общем виде в разных вариантах, в частности:
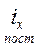 =
= 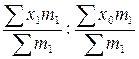 или
или 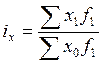 .
.
В первом варианте формулы используют в качестве весов абсолютные показатели (m), во втором варианте – относительные показатели (f).
В индексе постоянного состава устраняется влияние - m или f, т.е. второго фактора (изменение частей совокупности или структуры совокупности), и оценивается влияние изменения – x - первого фактора (изменение уровня индексируемого показателя).
Индекс постоянного состава показывает изменение средней величины показателя только за счет изменения уровня показателя в отдельных частях совокупности. Или можно сказать по-другому: этот индекс показывает изменение в среднем какого-либо показателя за счет изменения осредняемых уровней показателя.
Заметим, что разность между числителем и знаменателем каждого индекса, в частности 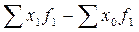 , показывает абсолютное изменение средней величины изучаемого показателя за счет изменения уровня показателя в отдельных частях совокупности.
, показывает абсолютное изменение средней величины изучаемого показателя за счет изменения уровня показателя в отдельных частях совокупности.
Влияние изменения частей совокупности (m) или доли (удельного веса) этих частей совокупности (f), т.е. изменения структуры совокупности, структурных сдвигов оценивается с помощью индекса структурных сдвигов
В общем виде этот индекс может быть записан так:
 =
= 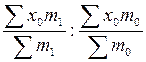 или
или 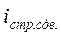 =
= 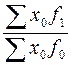 .
.
Первый вариант формулы предполагает использование индексируемого показателя - m - абсолютного показателя, второй вариант – использование – f - относительного показателя.
В индексе структурных сдвигов устраняется влияние – x – первого фактора и оценивается влияние изменения - m - или f - второго фактора.
Индекс структурных сдвигов показывает, как изменилась средняя величина показателя за счет изменения структуры совокупности. Или можно сказать по-другому, этот индекс показывает в какой мере влияет изменение состава, точнее структуры совокупности за изучаемый период на изменение среднего уровня показателя.
Разность между числителем и знаменателем каждого индекса, в частности 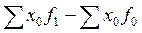 , показывает абсолютное изменение средней величины изучаемого показателя за счет изменения структуры совокупности.
, показывает абсолютное изменение средней величины изучаемого показателя за счет изменения структуры совокупности.
Заметим, что на практике индекс структурных сдвигов определяется исходя из установленной взаимосвязи индексов:
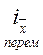 =
= 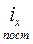
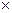
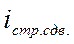 т.е.
т.е.
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 450; Нарушение авторских прав?; Мы поможем в написании вашей работы!