Основные законы распределения дискретных случайных величин

Показательное распределение.

Нормальное распределение.

Равномерное распределение.

Случайных величин.

Тема 5. Основные законы распределения случайных величин

Вопросы: 1. Основные законы распределения дискретных

1 Закон распределения Бернулли. Случайная величина Х, распределенная по закону Бернулли, принимает значения 1- успех или 0 - неудача, с вероятностями p и q соответственно (p+q=1).

xi
pi	q	p

2. Биномиальный закон распределения. Случайная величина X принимает значения: 0, 1, 2, 3, 4, 5,…, n, с вероятностью, определяемой по формуле Бернулли (1.24):

xi				…	к	…	n
pi				…		…

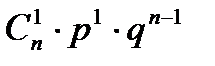
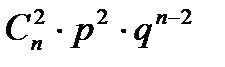
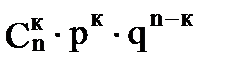
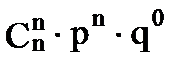
3. Закон распределения Пуассона. Случайная величина Х принимает бесконечное счетное число значений: 0, 1, 2, 3, 4, 5,…, к,…, с вероятностью, определяющейся по формуле Пуассона:

Р(Х=к)= 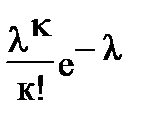, (2.2)

где l>0 - параметр распределения Пуассона.

xi				…	к	…
pi				…		…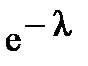

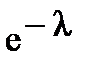
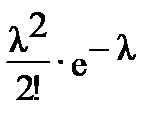
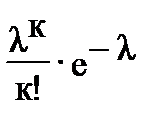
При n 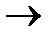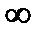и p 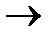0 биномиальный закон приближается к закону распределения Пуассона, где l=np.

4. Геометрический закон распределения. Пусть P(А)=p- вероятность наступления события А в каждом опыте, соответственно, q=1-p - вероятность не наступления события А (схема Бернулли).

Вероятность появления к - неудач до первого наступления события А определяется по формуле:

P(X=m)=p×q^m. (2.3)

Случайная величина Х распределенная по геометрическому закону принимает значения: 0,1,2,…,к,…, с вероятностью, определяемой по формуле (2.3):

xi				…	m	…
рi	p	pq	pq^2	…	Pq^m	…

5. Геометрический закон распределения сдвинутый на единицу.

Вероятность наступления события А в m-ом опыте определяется по формуле:

P(X=к)=p×q^m-1. (2.4)

Случайная величина Х - распределенная по геометрическому закону, сдвинутому на 1 (геометрический закон +1), означает число опытов до первого появления события А и принимает значения: 1, 2,…,к,…, с вероятностью, определяемой по формуле (2.4):

xi				…	к	…
рi	p	pq	pq^2	…	pq^к-1	…

6. Отрицательное биномиальное распределение. Если производится ряд независимых опытов в каждом из которых событие А появляется с вероятностью р, до получения m успехов (m=0,1,2,…),то при этом вероятность Х=к "неудачных" опытов можно определить по формуле:

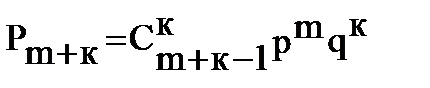(к = 0,1,2,...). (2.5)

Вероятность появления к-неудач, до получения m-успехов совпадает с m-ым членом разложения выражения q^к(1-р)^-к по степеням р, т.е. отрицательного бинома (отсюда и название):

.

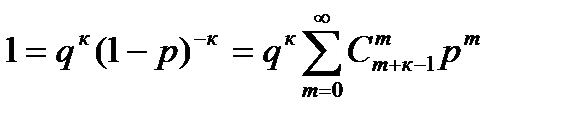Распределение определяется двумя параметрами «m» и «р».

2) Равномерное распределение

Случайная величина X распределена по равномерному (прямоугольному) закону, если ее функция плотности вероятностей принимает постоянное значение на промежутке (a.b) и равна нулю вне его.

Дифференциальная функция равномерного закона на интервале (a,b)

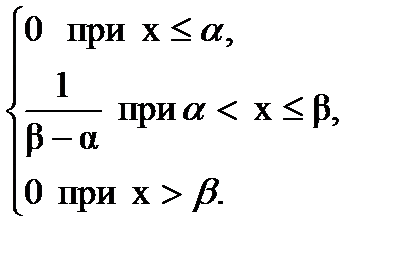(4.1)

Интегральная функция равномерного закона на интервале (a,b) (рис.11):

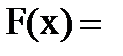
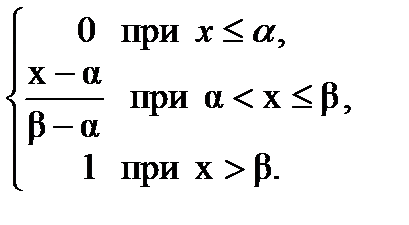(4.2)

Основные числовые характеристики равномерного закона:

1. Математическое ожидание:

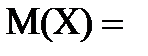
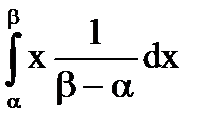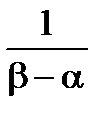
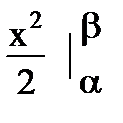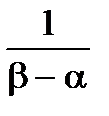
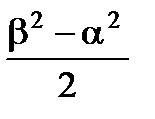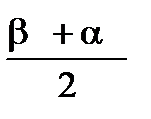= = == = . (4.3)

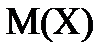совпадает, в силу симметрии распределения, с медианой.

2. Моды равномерное распределение не имеет.

3. Дисперсия: = =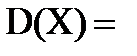

= = - = -

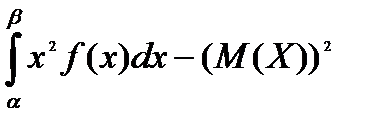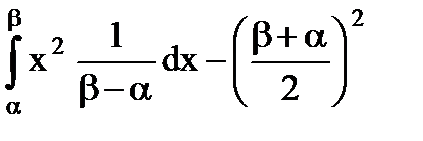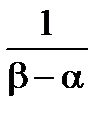
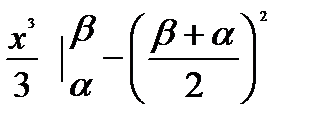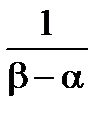
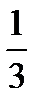
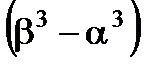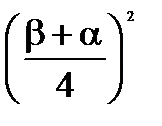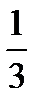
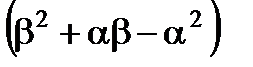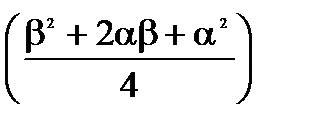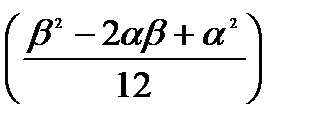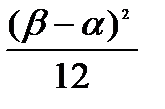- = = . (4.4)

Отсюда, среднее квадратическое отклонение 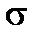(x)= 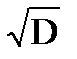= 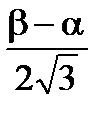. (4.5)

6. Вероятность попадания случайной величины в заданный интервал (a;b).

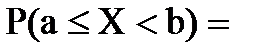
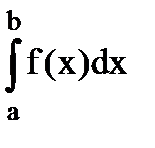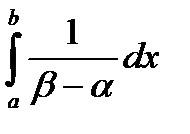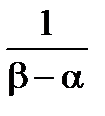
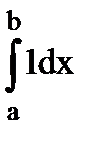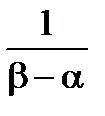
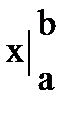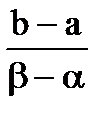= = = = . (4.6)

Дата добавления: 2014-11-20