Специальные законы распределения

1. c² -распределение Пирсона. Пусть X₁, X₂, …,X_n одинаково распределенные по нормальному закону случайные величины, являющиеся взаимно-независимыми, для которых математическое ожидание равно нулю, а среднеквадратическое отклонение 1, тогда сумма квадратов этих случайных величин носит название случайной величины χ² - xu-квадрат с n=n степенями свободы:

(5.8)

При ν=1 (учитывая пример) дифференциальная функция c²:

Дифференциальная функция распределения χ² с n=n степенями свободы

задаётся формулой

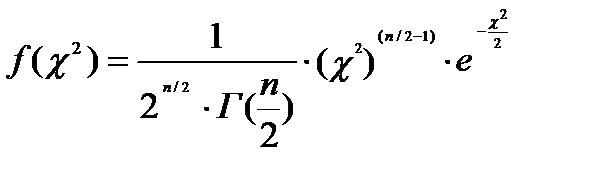, (5.9)

где Г(x) -гамма, функция Эйлера.

Г(x)= , при R₊; если nÎZ, то Г(n+1)=n!

С возрастанием числа степеней свободы n = n, распределение χ² медленно приближается к нормальному закону распределения. На практике используют обычно не плотность вероятности, а квантили распределения (прил. 2).

2. t– распределение Стьюдента. Это распределение имеет большое значение при статистических вычислениях, связанных с нормальным законом распределения, где s – неизвестный параметр распределения и подлежит определению из опытных данных, например, при статистической обработке наблюдений с неизвестной точностью.

Пусть X, X₁, X₂,…,X_k − независимые нормально распределённые случайные величины с нулевыми математическими ожиданиями и одинаковыми дисперсиями. Безразмерная величина t:

t = = , (5.10)

называется дробью Стьюдента.

Ее распределение не зависит от в силу ее безразмерности. Дифференциальная функция t-распределения с n=k степенями свободы имеет вид:

f(t)= 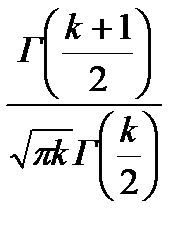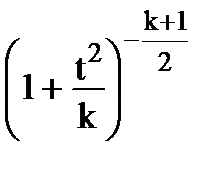. (5.11)

t-распределение Стьюдента, которое быстрее, чем χ² стремится к нормальному.

3. F- распределение Фишера-Снедекора.

Пусть X₁, X₂, …,X_m и Y₁, Y₂, …,Y_n одинаково распределенные по нормальному закону случайные величины, являющиеся взаимно-независимыми, для которых математическое ожидание равно нулю, а среднеквадратическое отклонение равно единице.

Рассмотрим дробь Фишера: F(m, n)= 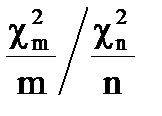, (5.12)

она имеет F - распределение с n₁=m - числом степеней свободы числителя, и n₂=n - числом степеней свободы знаменателя ((m, n) степенями свободы), которое называется распределением Фишера-Снедекора.)

Распределения c² - Пирсона, t - Стьюдента, F - Фишера-Снедекора нашли широкое применение в математической статистике, в частности при проверке статистических гипотез и в дисперсионном анализе.

Дата добавления: 2014-11-20