Основные методы вычисления неопределенного интеграла

Свойства неопределенного интеграла

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

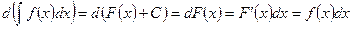(8.4)

2. Производная от неопределенного интеграла равна подынтегральной функции.

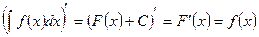(8.5)

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.

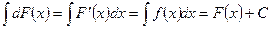(8.6)

4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от каждого слагаемого в отдельности, т.е.:

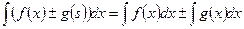(8.7)

5. Постоянный множитель можно вынести за знак неопределенного интеграла, т.е.:

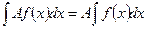(8.8)

Таблица интегралов

1.

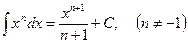
2.

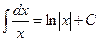
3.

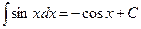
4.

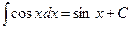
5.

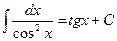
6.

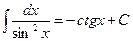
7.

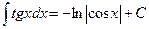
8.

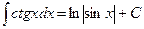
9.

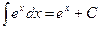
10.

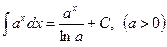
11.

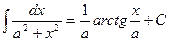
12.

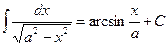
13.

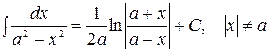
14.

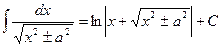
Пусть требуется найти неопределенный интеграл 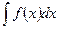, причем непосредственно подобрать первообразную не представляется возможным, но известно, что она существует. В этом случае применяются различные методы интегрирования, благодаря которым исходный интеграл можно привести к интегралу табличного вида. Рассмотрим некоторые из этих методов.

1. Метод непосредственного интегрирования. Используя свойства неопределенного интеграл, а также выполняя элементарные математические преобразования подынтегральной функции, исходный интеграл можно привести к неопределенному интегралу табличного вида.

Пример 8.2. Найти неопределенный интеграл .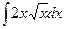

Используя пятое свойство неопределенного интеграла, вынесем за знак интеграла постоянную 2. Затем, выполняя элементарные математические преобразования, приведем подынтегральную функцию к степенному виду:

.

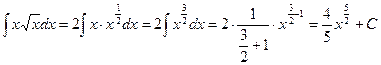2. Замена переменной. Пусть требуется найти неопределенный интеграл 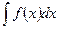. Сделаем замену в подынтегральном выражении, положив 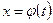, где 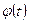— монотонная непрерывная функция, которая имеет непрерывную производную. Тогда 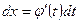. В этом случае имеет следующее равенство:

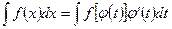(8.9)

Пример 8.3. Найти неопределенный интеграл 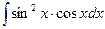, используя метод замены переменной.

Сделаем замену переменной 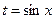, тогда 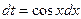. Исходный интеграл примет вид:

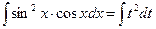
Таким образом, мы получили неопределенный интеграл табличного вида: степенная функция. Используя правило нахождения неопределенного интеграла от степенной функции (см. п.1 в таблице интегралов), найдем:

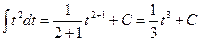
Сделав обратную замену, получим окончательный ответ:

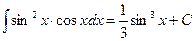
3. Интегрирование по частям. Пусть 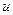и 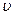— две дифференцируемые функции от переменной 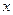. Тогда дифференциал произведения вычисляется по формуле:

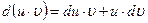(8.10)

Интегрируя, получим:

(8.11)

Отсюда:

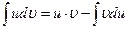(8.12)

Последняя формула называется формулой интегрирования по частям.

Пример 8.4. Найти неопределенный интеграл 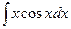, используя метод интегрирования по частям.

Введем следующие обозначения:

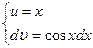(8.13)

Тогда дифференцируя первое выражение и интегрируя второе, получим:

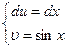(8.14)

Теперь подставив в формулу (8.12) введенные нами обозначения (8.13) и (8.14), получим:

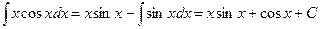
4. Интегралы от некоторых функций, содержащих квадратный трехчлен.

Рассмотрим следующие случаи:

а) В знаменателе интегрируемой функции квадратный трехчлен f(x) = .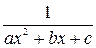

Преобразуем его, выделив полный квадрат.

.

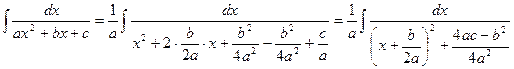Введем обозначение 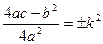. Таким образом, данный интеграл приобретает вид:

.

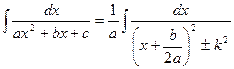Сделаем в последнем интеграле замену переменной:

,

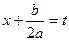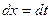
Получим:

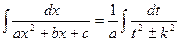. Это – табличный интеграл.

Пример 8.5.

Вычислить интеграл:

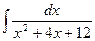
б) Подынтегральная функция имеет вид 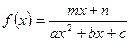. Произведем тождественные преобразования:

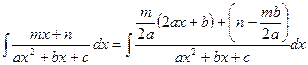
Таким образом, исходный интеграл можно представить в виде суммы:

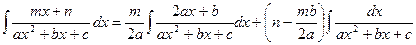
Как вычислять второй интеграл, мы рассмотрели в пункте 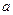; обозначим его через 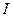. В первом интеграле сделаем замену переменной:

,

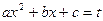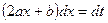
Таким образом:

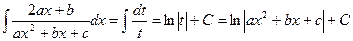
Окончательно получим:

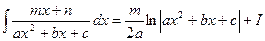
Пример. 7.6

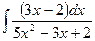
Приложения определенного интеграла

Дата добавления: 2014-11-20