Линейные уравнения первого порядка

Определение 12.9. Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной. Оно имеет вид:

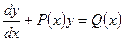(12.29)

где 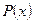и — заданные непрерывные функции от 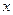(или постоянные).

Решение линейного уравнения:

Будем искать решение уравнения (12.29) в виде произведения двух функций от :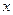

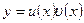. (11.30)

Одну из этих функций можно взять произвольной, другая определится на основании уравнения (12.29). Дифференцируя обе части равенства (12.30), находим:

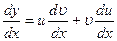(12.31)

Подставляя полученное выражение производной 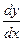в уравнение (12.29), будем иметь:

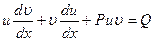(12.32)

или:

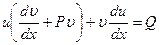(12.33)

Выберем функцию такой, чтобы:

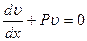(12.34)

Разделяя переменные в этом дифференциальном уравнении относительно функции 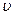, находим:

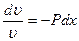(12.35)

Интегрируя, получаем:

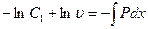
Или:

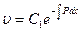
Так как нам достаточно какого-нибудь отличного от нуля решения уравнения (12.34), то за функцию 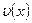возьмем:

Очевидно, что 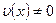. Подставляя найденное значение 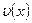в уравнение (12.33), получим:

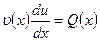
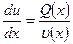
Отсюда:

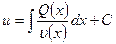(12.36)

Подставляя в формулу (12.30), окончательно получим:

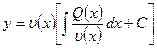(12.37)

Пример 12.9.

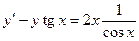
Решение:

Данное уравнение является линейным, так как содержит искомую функцию и ее производную в первой степени и не содержит их произведений. Применяем подстановку 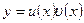. . 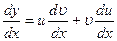Подставляя у и 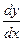в исходное уравнение, получим:

.

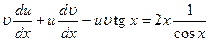Группируем первое и третье слагаемые и выносим 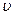за скобку:

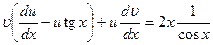(12.38)

Так как искомая функция у представлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию 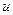так, чтобы выражение, стоящее в круглых скобках левой части равенства (12.38), обращалось в нуль, т.е., чтобы имело место равенство

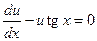. (12.39)

Тогда уравнение (12.38) принимает вид:

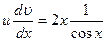(12.40).

Уравнение (12.39) является уравнением с разделяющимися переменными относительно u и x. Решим его:

; ; ; .

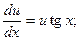
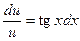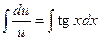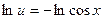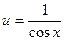Чтобы равенство (12.39) имело место, достаточно найти одно какое-либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находим то частное решение, которое соответствует значению произвольной постоянной 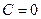. Подставив в (12.40) найденное выражение для u, получим: 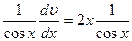; ; 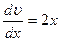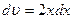. Интегрируя, имеем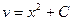

Теперь можно получить общее решение исходного уравнения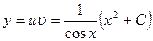

Дата добавления: 2014-11-20