Дифференциальные уравнения второго порядка, допускающие понижение порядка

Определение дифференциального уравнения второго порядка

Обыкновенные дифференциальные уравнения второго порядка

План

1. Определение дифференциального уравнения второго порядка

2. Дифференциальные уравнения второго порядка, допускающие понижение порядка

3. Линейные однородные уравнения

4. Линейные однородные уравнения второго порядка с постоянными коэффициентами

5. Линейные неоднородные дифференциальные уравнения второго порядка

Дифференциальные уравнения вида:

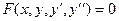(13.1)

называются уравнениями второго порядка.

Будем рассматривать уравнения, которые можно записать в виде, разрешенном относительно второй производной:

(13.2)

В некоторых случаях решения дифференциальных уравнений может быть сведено к последовательному решению двух дифференциальных уравнений первого порядка. Рассмотрим три случая.

1) Если дифференциальное уравнение имеет следующий вид:

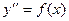(13.3)

то оно решается последовательным интегрированием.

Пример 13.1.

Найти общее решение данного дифференциального уравнения:

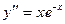
Найдем сначала :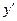

. Данный интеграл решается методом интегрирования по частям.

Введем обозначения: 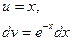, тогда 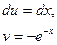и

Теперь найдем искомую функцию y:

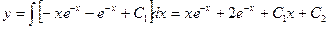
2) Если в запись уравнения не входит искомая функция y(x), т.е.:

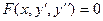(13.4)

то такое уравнение можно решить, если найти сначала вспомогательную функцию .

Пример 13.2

Введем вспомогательную функцию . Исходное уравнение примет следующий вид:

. Полученное уравнение является однородным уравнением первого порядка. Последнее уравнение можно записать в виде:

(13.5)

Пусть . Отсюда:

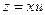(13.6)

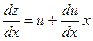(13.7)

Подставим (13.5) и (13.6) в (13.4), получим:

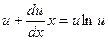. Отсюда:

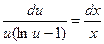. Интегрируем левую и правую часть данного уравнения:

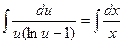. Левый интеграл решается методом замены переменной:

В результате интегрирования находим:

или . Отсюда:

. Вернемся к переменной y:

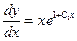. Следовательно:

3) Если в уравнение не входит переменная x:

(13.8)

то порядок уравнения можно понизить, если за независимую переменную взять y, а неизвестную функцию – z=y′.

Дата добавления: 2014-11-20