Практические работы

Рассмотрим подробнее спецификации каждой практической работы.

2.1. Практическая работа №1 «Решение уравнений с одной переменной»

Обязательных методов
Баллов за обязательные методы
Дополнительных методов
Баллов за дополнительные методы
Количество вариантов

В ходе данной практической работы необходимо реализовать ряд методов решения уравнений

f (x) = 0, (2.1.1)

где x 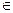[a, b] – скалярный аргумент функции f. При этом предполагается, что отделение корней уже произведено, т.е. на отрезке [a, b] находится только одно решение уравнения (2.1.1) ξ 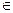[a, b], или, другими словами, только один нуль функции f (x), т.е. f (ξ) ≡ 0. В этом случае выполняется условие

f (a) f (b) ≤ 0. (2.1.2)

Решение должно быть найдено с абсолютной погрешностью по аргументу ε и/или абсолютной погрешностью по значению функции δ, т.е.

|ξ – x^*| < ε и/или (2.1.3)

| f (x^*)| < δ, (2.1.4)

где ξ – точное решение уравнения (2.1.1), а x^* – приближенное.

Зачем использовать две различные погрешности? Дело в том, что, в зависимости от вида функции, погрешность решения по аргументу и по значению функции могут не совпадать. Например, рассмотрим быстро растущую функцию. Из рисунка 2.1.1 видно, что даже если по аргументу требуемая точность решения достигнута, то по значению функции – нет. Такая же ситуация будет наблюдаться для быстро убывающей функции (т.е. для любой функции, имеющей на исследуемом отрезке большую производную).

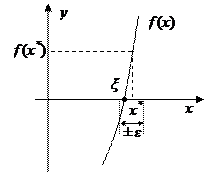
Рис. 2.1.1 – Пример функции с большим (по модулю) значением производной вблизи корня

Обратная ситуация будет наблюдаться для функции с малыми значениями производной – при достижении требуемой точности по значению функции, точность по аргументу достигнута не будет (рис. 2.1.2).

Для упрощения можно положить ε = δ. Так как точный корень нам неизвестен, то условие (2.1.3) в численных методах заменяют другими, альтернативными, условиями, которые мы рассмотрим ниже.

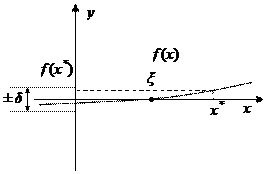
Рис. 2.1.2 – Пример функции с малым (по модулю) значением производной вблизи корня

Дата добавления: 2014-11-20