Интервальные методы

Методы решения

Для решения уравнения (2.1.1) необходимо реализовать три обязательных метода (дихотомии, хорд и Ньютона) и, по желанию, три дополнительных (комбинированный метод, метод итераций и золотого сечения).

Методы дихотомии, хорд и золотого сечения являются интервальными, т.е. их смысл заключается в уменьшении исходного интервала, содержащего корень, до тех пор, пока размеры интервала не окажутся соизмеримы с требуемой погрешностью.

Для этих методов интервалом поиска корня на некоторой k-й итерации будет являться отрезок [a_k, b_k], при этом a₀ = a, b₀ = b. Длина интервала в интервальных методах гарантированно уменьшается на каждой итерации решения, поэтому альтернативой условию (2.1.3) будет, очевидно, условие

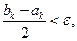(2.1.5)

т.к. погрешность определения корня не может превышать половины длины интервала.

В методе дихотомии интервал разбивается следующим образом. Вычисляется точка, расположенная в середине отрезка:

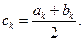(2.1.6)

Далее, согласно (2.1.2), проверяется, какому из интервалов – [a_k, с_k] или [с_k, b_k] – принадлежит корень. Т.е.,

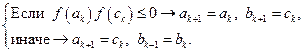(2.1.7)

В качестве k-го приближения корня берется точка

(2.1.8)

В методе хорд интервал разбивается другой точкой:

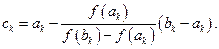(2.1.9)

Выбор интервала осуществляется согласно (2.1.7), а новое приближение корня совпадает с точкой c_k (x_k = c_k). Однако, в отличие от других интервальных методов, в методе хорд постоянное уменьшение длины интервала не гарантировано, поэтому погрешность рассчитывается по формуле итерационных методов (2.1.13).

В методе золотого сечения интервал разбивается двумя симметричными относительно границ интервала точками:

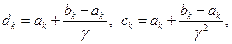(2.1.10)

где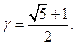

Для упрощения вычислений можно учесть упомянутую симметричность расположения точек c_k и d_k:

c_k – a_k = b_k – d_k. (2.1.11)

Далее, согласно (2.1.2), проверяется, какому из интервалов – [a_k, d_k] или [с_k, b_k] – принадлежит корень. Т.е.,

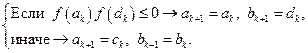(2.1.12)

Новое приближение корня вычисляется по формуле (2.1.8).

Дата добавления: 2014-11-20