Итерационные методы

Методы Ньютона (касательных) и итераций являются итеративными (итерационными), на основе некоторого приближения корня x_k они позволяют на каждой итерации получать новое приближение x_k+1. При этом используется информация о первой производной функции. Вместо условия (2.1.3) в итеративных методах оценивается расстояние между последним и предпоследним приближениями корня:

|x_k+1 – x_k| < ε. (2.1.13)

При этом нужно знать начальное приближение x₀, а дальнейшие приближения на каждой k+1-й итерации находятся по итеративной формуле:

x_k+1 = φ(x_k). (2.1.14)

В методе Ньютона начальное приближение выбирается в соответствии со следующим условием: если в некоторой точке x произведение f (x) f "(x) > 0, то точка x является подходящей для начала итерационного процесса. Проверяются границы интервала:

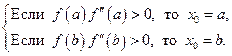(2.1.15)

На практике может наблюдаться ситуация, когда оба условия (2.1.15) не выполняются. В этом случае вместо второго условия можно использовать оператор «иначе», либо воспользоваться вторым критерием.

Если вторая производная функции не известна, можно воспользоваться другим критерием. Вычислим точку c по формуле (2.1.9), и далее

(2.1.16)

Если начальная точка определена неправильно, то найденное решение уравнения (2.1.1) может находиться за пределами отрезка [a, b].

Функция φ(x_k) в (2.1.14) для метода Ньютона выглядит следующим образом:

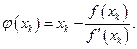(2.1.17)

В методе итераций, если выполняется неравенство |φ'(x)| < 1, процесс сходится независимо от выбора начальной точки. Поэтому можно брать любую из границ интервала, его середину и т.п. А функция φ(x_k) в (2.1.14) выглядит следующим образом:

(2.1.18)

В отличие от интервальных методов, длина исследуемого отрезка в которых на каждой итерации гарантированно уменьшается (например, для метода дихотомии – в два раза, для метода золотого сечения – в γ раз), в итеративных методах, в общем случае, расстояние между последовательными приближениями корня может иногда и увеличиваться. То же самое касается и значения функции в этих точках – оно может как уменьшаться, так и увеличиваться. Поэтому для некоторых функций условия (2.1.3) и (2.1.4) могут не выполняться в течение довольно большого числа итераций (или вообще никогда). В этом случае итерации следует прекращать при выполнении хотя бы одного условия.

Дата добавления: 2014-11-20