Метод ортогонализации

Метод ортогонализации лишен этого недостатка. Как видно из формул, приведенных ниже, деление на ноль он может дать только в том случае, если одна из строк матрицы U будет содержать только нули. А при выполнении условия (2.2.4) это невозможно.

Итак, сначала исходная матрица A преобразуется в расширенную матрицу A' размера (n+1)´(n+1):

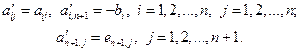(2.2.15)

Здесь e_n+1 – n+1-я строка единичной матрицы. Расширенный вектор x' дополняется еще одним компонентом, и его размер для расширенной системы составляет n+1. Сама же расширенная СЛАУ будет выглядеть так:

A' x' = 0. (2.2.16)

Чтобы расширенная система была эквивалентна исходной, последний компонент вектора x' должен быть равен единице, т.е.

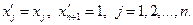(2.2.17)

Таким образом, имеем следующую расширенную систему:

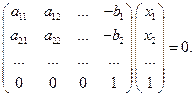
Далее последовательно находятся строки некоторых матриц U и Z. Их размер также составляет (n+1)´(n+1):

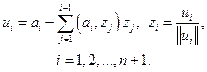(2.2.18)

Здесь a_i, u_i, z_i – соответствующие строки матриц A', U и Z. В скобках стоит скалярное произведение, а норма в данном случае – это квадратный корень из скалярного произведения вектора самого на себя, т.е. может быть вычислена по формуле (1.4).

После этого можем получить решение СЛАУ:

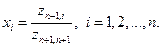(2.2.19)

Очевидно, что при программировании можно обойтись всего одной матрицей:

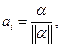где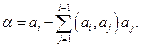

Дата добавления: 2014-11-20