Вычисление собственных чисел методом Данилевского

Методы решения

При аналитическом решении собственные числа матрицы находятся из решения уравнения

D(λ) = 0, (2.3.4)

где D(λ) = det(A – λE) – характеристический полином матрицы. После этого, согласно (2.3.1), можно найти собственные вектора, решая СЛАУ

(A – λE)x = 0. (2.3.5)

В данной практической работе для поиска собственных чисел и векторов мы будем использовать метод Данилевского. Суть его состоит в том, что исходная матрица A преобразуется в подобную ей матрицу Фробениуса P, имеющую следующий вид:

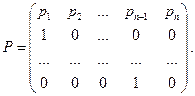
Делается это при помощи следующего преобразования подобия:

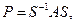(2.3.6)

где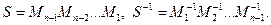

Таким образом, можно последовательно находить n–1 матрицу A^(k):

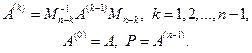(2.3.7)

А можно найти матрицы S (прямую и обратную) и затем сразу вычислить P по формуле (2.3.6). Такой способ эффективнее, т.к. не нужно хранить множество матриц M, произведение которых еще понадобятся для вычисления собственных векторов.

Матрицы M строятся следующим образом:

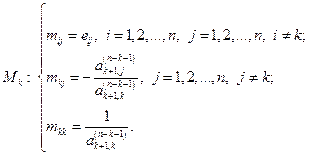(2.3.8)

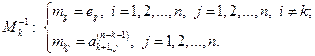(2.3.9)

Несложно доказать, что у подобных матриц собственные числа совпадают. Далее для матрицы P строится характеристический полином

D(λ) = det(P – λE) =

(–1)ⁿ[λⁿ – p₁λ^n–1 – p₂λ^n–2 – … – p_n]. (2.3.10)

Это полином степени n. Очевидно, что он имеет n корней λ₁, λ₂, …, λ_n. Некоторые из них могут быть кратными, при этом выполняется соотношение (2.3.2). Необходимо не только найти все корни полинома, но и определить их кратность (см. п. 2.3.1.3).

Дата добавления: 2014-11-20