Формат выходных данных. Формат входных данных

Формат входных данных

Вычисление обратных матриц

Обозначим как X неизвестные элементы обратной матрицы. Следовательно, нам необходимо решить систему

AX = E, (2.2.27)

где E – единичная матрица, т.е.

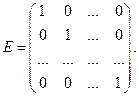
Все матрицы имеют размер n´n. Решение матричной системы (2.2.27) можно представить в виде решения n СЛАУ

Ax_i = e_i, i = 1, 2, …, n, (2.2.28)

где x_i, e_i – i-й столбец обратной и единичной матрицы соответственно.

Обратите внимание, что при вычислении обратной матрицы СЛАУ решается n раз, где n – порядок матрицы. При этом все треугольные матрицы в методах Гаусса и декомпозиции получаются одинаковыми, меняется только вектор свободных коэффициентов. Это нужно использовать для оптимизации вычислений в программе – все треугольные матрицы должны вычисляться только один раз.

Формат входного файла:

m	– тип задачи (в том порядке, в котором они перечислены выше);
n	– порядок матрицы;
a11…a1n [b1] a21…a2n [b2] ……………………… an1…ann [bn]	– коэффициенты матрицы и вектор свободных коэффициентов (при решении СЛАУ, т.е. при m = 1).

Формат выходного файла зависит от метода и типа задачи:

· Если используется метод Гаусса, то в любом случае в выходной файл выводятся матрицы A⁽¹⁾, A⁽²⁾, …, A⁽ⁿ⁾. Если решалась система СЛАУ, то еще и вектора b⁽¹⁾, b⁽²⁾, …, b⁽ⁿ⁾. Если вычислялась обратная матрица – вектора e₁⁽ⁿ⁾, e₂⁽ⁿ⁾, …, e_n⁽ⁿ⁾.

· Если используется метод декомпозиции, то в любом случае выводятся матрицы B и C. Если решалась система СЛАУ, то вектор y. Если вычислялась обратная матрица – вектора y₁, y₂, …, y_n.

· Если используется метод ортогонализации, то в любом случае выводится расширенная матрица A'. При решении СЛАУ выводятся матрицы U и Z. Если вычислялась обратная матрица – матрицы U₁, Z₁, U₂, Z₂, …, U_n, Z_n.

· Для итерационных методов выводятся матрицы α и вектора β (для каждой решаемой СЛАУ).

При решении СЛАУ в файл выводятся:

x^*	– вектор решения;
ε	– вектор невязки;
||ε||	– норма вектора невязки.

При поиске определителя – его значение. При вычислении обратной матрицы – следующие величины:

X	– обратная матрица;
ε	– матрица невязки (AX – E);
||ε||	– норма матрицы невязки.

2.3. Практическая работа №3 «Вычисление собственных чисел и собственных векторов»

Обязательных методов
Баллов за обязательные методы
Дополнительных методов
Баллов за дополнительные методы
Количество вариантов

Собственные числа и вектора квадратной матрицы являются ее важными характеристиками, использующимися в различных формах математического анализа. Собственное число матрицы λ_i и соответствующий ему собственный вектор x_i удовлетворяют следующему соотношению:

Ax_i = λ_ix_i. (2.3.1)

У квадратной матрицы размерности n имеется n собственных чисел и векторов. Некоторые из них могут быть кратными (т.е. совпадающими). Таким образом, квадратная матрица размерности n имеет m различных собственных чисел λ_i и соответствующих им собственных векторов x_i кратности k_i. При этом

(2.3.2)

Отметим также, что от умножения собственного вектора матрицы на скаляр c он не перестает быть ее собственным вектором:

A(cx_i) = λ_i(cx_i) Þ cAx_i = cλ_ix_i Þ Ax_i = λ_ix_i. (2.3.3)

Дата добавления: 2014-11-20