
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы решения
|
|
|
|
Данная практическая работа выполняется по вариантам. Первый вариант – это метод Ньютона, второй – Лагранжа. Эти полиномы являются степенными.
Известно, что через две точки можно провести одну и только одну прямую, через три – одну и только одну параболу и т.д. Поэтому, через n+1 точку {xi} можно провести одну и только одну кривую порядка n. Отсюда можно сделать два вывода. Во-первых, чем больше количество точек в заданной сетке, тем выше, в общем случае, будет степень полинома P(x). Именно этим и объясняется осциллирующее поведение полиномов Ньютона и Лагранжа при большом количестве точек – просто их вид становится слишком сложным. Отметим, что для других интерполирующих полиномов это может быть и не так. Например, МНК, независимо от количества точек, дает полином, для которого выполняется условие (2.5.3). Т.е., если в качестве линейно-независимых функций взять φi(x) = xi, i = 1, 2, …, m, то можно построить, например, кубический полином для любого количества точек (при m = 3). Порядок у него ниже, поэтому он более гладкий. При m = n МНК становится обычным интерполяционным полиномом. Во-вторых, полиномы Ньютона и Лагранжа совпадают, т.е. это просто две формы записи одного и того же полинома, и их можно преобразовать к следующему виду:
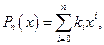
где ki – некоторые константы. Индекс n у полинома указывает на его порядок.
При этом, каждым вариантом необходимо реализовать 6 задач:
1. Вычисление полинома на равномерной сетке;
2. Вычисление полинома на неравномерной сетке;
3. Вычисление первой производной полинома на равномерной сетке;
4. Вычисление первой производной полинома на неравномерной сетке;
5. Вычисление второй производной полинома на равномерной сетке;
6. Вычисление второй производной полинома на неравномерной сетке;
При использовании равномерной сетки вводится новая переменная
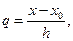 (2.5.9)
(2.5.9)
и подставляется в полином и его производные. Таким образом, получается, что они зависят только от q, а x и {xi} явным образом в них не входят. Т.е. имеем P(q). Получить его можно самостоятельно, сделав замену (2.5.9) в полиноме P(x).
Выигрыш состоит в том, что не нужно хранить в памяти узлы сетки {xi}, поэтому ее используется примерно в два раза меньше.
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 363; Нарушение авторских прав?; Мы поможем в написании вашей работы!