Федковича

ВОГЕЛЯ

ДВУХЧЛЕННАЯ

ЧАСТНЫЕ ИНДИКАТОРНЫЕ ЗАВИСИМОСТИ

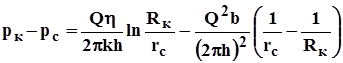. 66

Дебит находится как положительный корень квадратного уравнения (66).

, 67

где Q_max – максимально возможный дебит при р_с ®0; V_c- константа Вогеля.

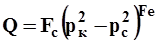, 68

где F_c, Fe –константы Федковича.

2.8. ВЛИЯНИЕ РАДИУСА СКВАЖИНЫ НА ЕЁ ПРОИЗВОДИТЕЛЬНОСТЬ

Определим дебит в двух крайних случаях: по закону Дарси и по закону Краснопольского развитого нелинейного течения. Тоже самое сделаем и в случае радиально-сферического течения. Если примем радиус одной скважины r_с, а другой - r_c^/= xr_c и, соответственно, дебиты G и G^/, а их отношение обозначим через у=G/G^/, то получим следующие формулы для вычисления предельных значений у

Закон	Тип потока
фильтрации	плоско-радиальный	радиально-сферический
Дарси		у=х
Краснопольского

Из таблицы видно, что при сохранении закона Дарси в плоско-радиальном потоке влияние радиуса скважины на дебит невелико (необходимо увеличение радиуса в 10 раз, чтобы дебит вырос на 20%). Если же фильтрация нелинейна, то влияние r_c на G усиливается. Для сферически-радиального потока дебит скважины зависит от радиуса в большей степени, особенно при нелинейном законе фильтрации. Таким образом, расширение забоя скважины способствует увеличению производительности. При торпедировании забоя, гидравлическом разрыве пласта и других способах воздействия на призабойную зону образуются и расширяются трещины, что способствует нарушению закона Дарси и, следовательно, усилению влияния радиуса скважины на приток к ней жидкости.

Дата добавления: 2014-11-08