Метод наименьших квадратов

Если регрессия линейна, то речь ведут о линейной регрессии. Модель линейной регрессии является наиболее распространенным (и простым) уравнением зависимости между экономическими переменными. Кроме того, построенное линейное уравнение может быть начальной точкой эконометрического анализа.

Из предыдущих рассуждений ясно, что парная линейная регрессия (теоретическое линейное уравнение регрессии) представляет собой линейную функцию между условным математическим ожиданием 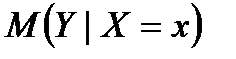зависимой переменной Y и одной переменной X:

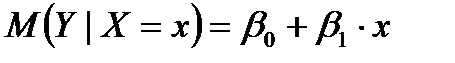. (1.1)

Отметим, что принципиальной в данном случае является линейность по параметрам 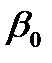и 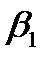уравнения. Для отражения того факта, что каждое индивидуальное значение 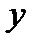отклоняется от соответствующего условного математического ожидания, необходимо ввести в соотношение (1.1) случайное слагаемое :

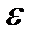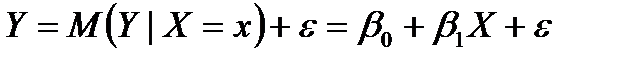. (1.2)

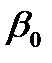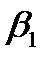Соотношение (1.2) называется теоретической линейной регрессионной моделью; и ‒ теоретическими параметрами (теоретическими коэффициентами) регрессии; 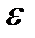‒ случайным отклонением (случайной ошибкой).

Для определения значений теоретических коэффициентов регрессии необходимо знать и использовать все значения переменных X и Y генеральной совокупности, что практически невозможно. Таким образом, нужно уметь оценивать коэффициенты 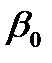и 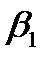на основе статистических данных (выборки) 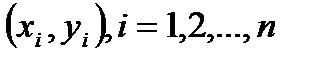, переменных X и Y. Тогда по выборке ограниченного объема мы сможем построить так называемое эмпирическое (выборочное) уравнение регрессии

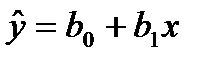, (1.3)

где 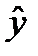‒ оценка условного математического ожидания 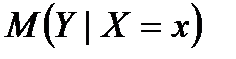; 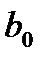и 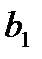‒ оценки неизвестных параметров 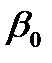и 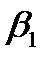, называемые эмпирическими (выборочными) коэффициентами регрессии. В каждом конкретном наблюдении выборки имеем 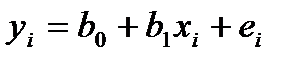, где отклонение 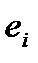‒ оценка теоретического случайного отклонения .

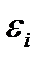В силу несовпадения статистической базы для генеральной совокупности и выборки оценк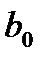и и 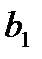практически всегда отличаются от истинных значений коэффициентов 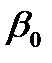и 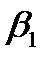, что приводит к несовпадению эмпирической и теоретической линий регрессии. Различные выборки из одной и той же генеральной совокупности обычно приводят к определению отличающихся друг от друга оценок. Задача состоит в том, чтобы по конкретной выборке 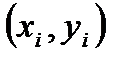, , 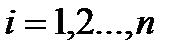найти оценк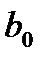и и 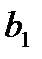неизвестных параметров 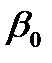и 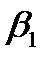так, чтобы построенная линия регрессии являлась бы наилучшей в определенном смысле среди всех других прямых. Другими словами, построенная прямая 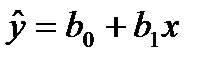должна быть «ближайшей» к точкам наблюдений по их совокупности.

Рассмотрим задачу «наилучшей» аппроксимации набора наблюдений 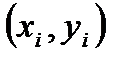, 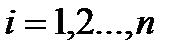линейным уравнением (1.3). На рис. 2 приведены диаграмма рассеяния наблюдений из примера 1 и линия регрессии. Величина 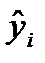описывается как расчетное значение переменной y, которое соответствует 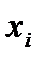. Наблюдаемые значения 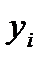не лежат в точности на линии регрессии, т.е. не совпадают с расчетными значениями 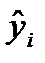. Разность 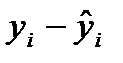обозначим .

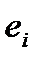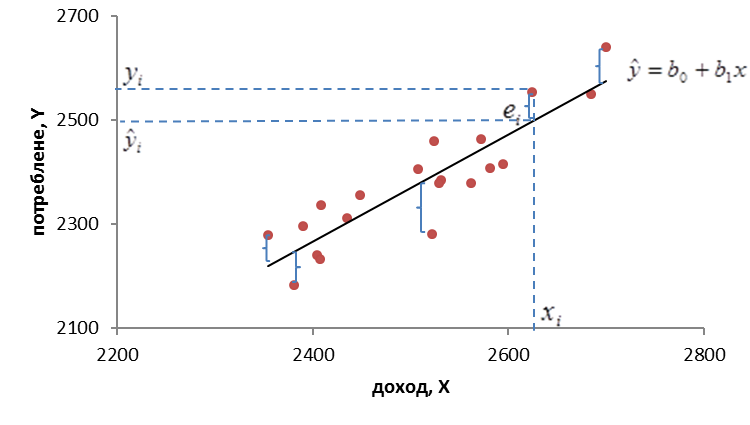
Рис. 2

Коэффициенты 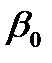и 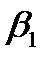будем оценивать по выборке с помощью метода наименьших квадратов (МНК, именно этот метод используется в Microsoft Excel). Суть МНК заключается в минимизации суммы квадратов отклонений наблюдаемых значений объясняемой переменной от ее расчетных значений, т.е. необходимо найти минимум квадратичной функции двух переменных 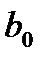и :

.

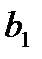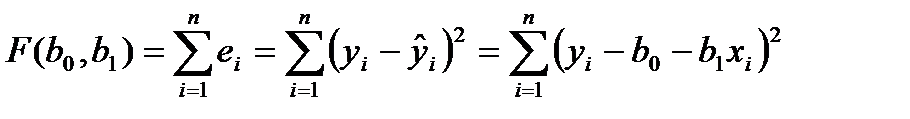Необходимым условием существования минимума функции двух переменных является равенство нулю ее частных производных по переменным 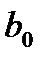и :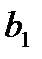

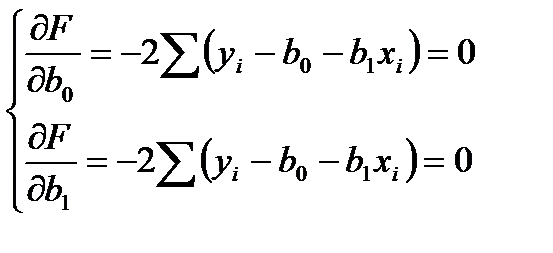
Разрешив полученную систему относительно 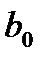и 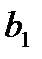, получим формулы для вычисления оценок парной линейной регрессии:

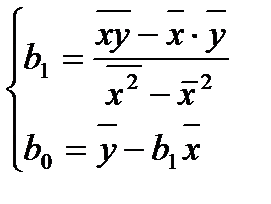, (1.4)

где , , , .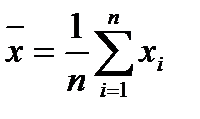

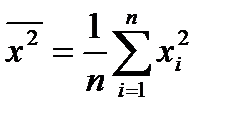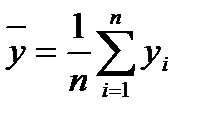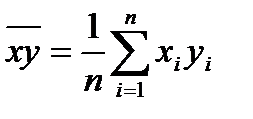Замечания.

1) Нетрудно доказать, что имеет место соотношени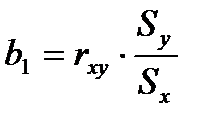е , где 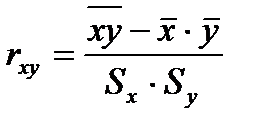‒ выборочный коэффициент корреляци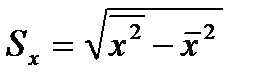и; и 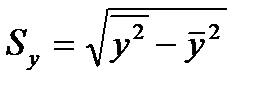‒ стандартные отклонения. Таким образом, коэффициент регрессии пропорционален коэффициенту корреляции.

2) Линия регрессии проходит через точку 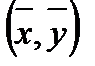, и выполняются равенства , .

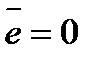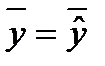3) В настоящее время оценк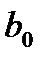и и 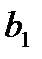обычно не вычисляют «вручную» по формулам (6). Для этого можно воспользоваться, например, настройкой «Пакет анализа» в приложении Excel (см. пример ниже).

Дата добавления: 2014-11-20