Чистый сдвиг

Чистым сдвигом называется такое напряженное состояние, когда из бруса можно выделить такой элемент, по двум взаимно перпендикулярным граням которого действуют только касательные напряжения. Такие грани называются площадками чистого сдвига.

Рассмотрим частный случай одновременного действия на элемент бурса во взаимно перпендикулярных направлениях равных по величине и противоположных по знаку (растягивающих и сжимающих) нормальных напряжений 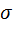(Рис.1.2, а).

а) б) в)

Рис.1.2

Определим напряжения в наклонном сечении n-n.

Составляя уравнения равновесия выделенной части элемента (рис.1.2, б), найдем:

= (sin² 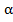– cos² 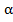)_, , (1.3)

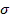при , = 0, .

Таким образом, элемент, стороны которого составляют углы по 45⁰ с направлениями нормальных напряжений, равных по величине и противоположных по знаку, находятся в условиях чистого сдвига (рис.1.2, в).

Другим примером, иллюстрирующим состояние чистого сдвига, может служить кручение тонкостенной трубки (рис. 1.3, а)

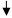
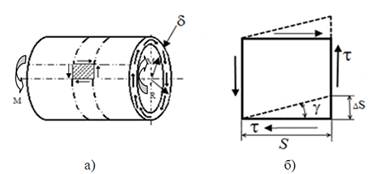
Рис.1.3

На гранях элемента стенки трубки действуют только касательные напряжения (Рис.1.3, б)

τ = , (1.4)

где R – средний радиус трубки;
δ - толщина,

2πR – площадь поперечного сечения.

Рассмотрим деформацию элемента, находящегося в условиях чистого сдвига.

Величина ∆S, на которую сдвинулась грань элемента относительно своего первоначального положения (рис.1.3, б) называется абсолютным сдвигом. Угол 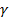, на который поворачивается эта грань, носит название угла сдвига или относительного сдвига. Угол сдвига в пределах упругой деформации - малая величина, поэтому тангенс угла примерно равен самому углу, т.е.

γ≈ tgγ = . (1.5)

Дата добавления: 2014-11-20