
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Напряжения и перемещения при кручении вала круглого сечения
|
|
|
|
Примем следующие допущения: поперечные сечения вала при действии на него внешних скручивающих моментов поворачиваются в своей плоскости как жесткие диски (гипотеза плоских сечений или Бернулли); в поперечных сечениях возникают только касательные напряжения. Формулы, полученные на основе этих допущений, подтверждаются опытами.
Выделим из вала бесконечно близкими двумя поперечными сечениями и двумя цилиндрическими поверхностями элементарный цилиндр, показанный на рис.2.3.
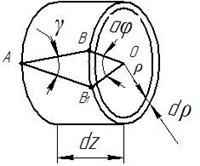
Рис.2.3.
Правое сечение цилиндра поворачивается относительно левого при кручении вала на угол 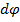 . Угол
. Угол 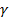 на который поворачивается отрезок АВ на поверхности цилиндра представляет собой угол сдвига.
на который поворачивается отрезок АВ на поверхности цилиндра представляет собой угол сдвига.
Из рисунка видно, что ВВ1 = 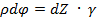 , отсюда получаем
, отсюда получаем
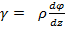 = ρ
= ρ 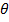 . (2.1)
. (2.1)
Здесь обозначено 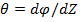 .
.
Величину 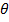 называют относительным углом закручивания.
называют относительным углом закручивания.
По закону Гука при сдвиге (см.формулу 1.6.)
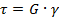 , (2.2)
, (2.2)
здесь G – модуль сдвига.
Сравнивая выражения (2.1) и (2.2), получим следующее соотношение между касательным напряжением 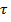 в поперечном сечении вала и относительным углом закручивания
в поперечном сечении вала и относительным углом закручивания 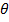 :
:
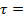 G
G 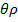 . (2.3)
. (2.3)
Отметим, что формула (2.1) отражает геометрическую сторону задачи (условие совместности деформаций и перемещений), формула (2.2.) – физическую сторону (закон Гука), формула (2.3.) – результат рассмотрения геометрической и физической сторон задачи.
Рассмотрим статическую сторону задачи. Выразим крутящий момент через касательные напряжения, суммируя элементарные моменты (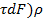 (Рис.2.4.)
(Рис.2.4.)
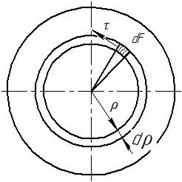
Рис.2.4
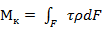 . (2.4)
. (2.4)
Подставив в (2.4) напряжение 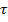 из (2.3) получим:
из (2.3) получим:
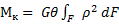 . (2.5)
. (2.5)
Введем обозначение:
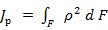 . (2.6)
. (2.6)
Интеграл (2.6.) представляет собой геометрическую характеристику и называется полярным моментом инерции сечения, его размерность м4. Таким образом
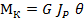 . (2.7)
. (2.7)
Отсюда относительный угол закручивания
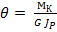 . (2.8)
. (2.8)
Учитывая, что 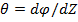 , получим выражение для определения угла закручивания
, получим выражение для определения угла закручивания
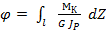 , (2.9)
, (2.9)
где l - расстояние между сечениями, между которыми определяется взаимный угол поворота.
В случае, если диаметр вала и крутящий момент на длине l постоянны, то
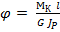 . (2.10)
. (2.10)
Произведение GJp называется - жесткостью поперечного сечения круглого вала при кручении,
G JP / l - жесткость вала длиной l.
Подставляя (2.8) в (2.3) получим
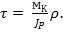 (2.11)
(2.11)
Из формулы (2.11) следует, что касательные напряжения в поперечных сечениях вала при кручении распределяются по линейному закону вдоль любого радиуса.
При ρ=0 (в центре сечения) 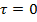 , максимального значения напряжения достигают в поперечном сечении вала у его поверхности при ρ = R.
, максимального значения напряжения достигают в поперечном сечении вала у его поверхности при ρ = R.
Эпюра касательных напряжений показана на рис. 2.5
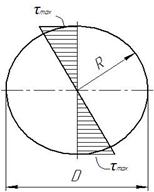
Рис.2.5.
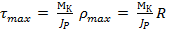 . (2.12)
. (2.12)
Отношение Jmax / ρmax = Wp называется полярным моментом сопротивления сечения.
С учетом этого обозначения запишем выражение для максимального касательного напряжения в виде:
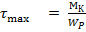 . (2.13)
. (2.13)
Отметим, что для круглого сечения
 , (2.14)
, (2.14)
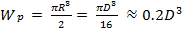 . (2.15)
. (2.15)
Для кольцевого сечения:
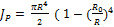 ) =
) = 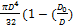 4)
4) 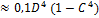 , (2.16)
, (2.16)
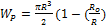 4)=
4)= 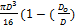 4)
4) 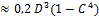 , (2.17)
, (2.17)
где Ro, Do – внутренний радиус и диаметр кольцевого сечения,
С= Do/ D = Ro/R.
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 1813; Нарушение авторских прав?; Мы поможем в написании вашей работы!