Статически неопределимые задачи при кручении

Расчеты на прочность и жесткость при кручении, как правило, начинают с определения внутренних силовых факторов (крутящих моментов). Если крутящие моменты не могут быть определены методом сечений с помощью одних только уравнений равновесия, то такая задача является статически неопределимой.

Для ее решения кроме статической стороны задачи, необходимо рассмотреть геометрическую сторону - составить условия совместности перемещений, и физическую - выразить перемещения (углы закручивания) через крутящие моменты по формуле Гука. Рассмотрим решение статически неопределимых задач на примерах.

Пример 2.4. Определить из расчетов на прочность и жесткость допускаемое значение скручивающего момента М для вала круглого сечения, жестко заземленного обоими концами и нагруженного, как показано на рис.2.17, а.

Рис.2.17

Допускаемое касательное напряжение [ 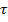]= 80 МПа, допускаемый угол закручивания [ 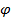] = 0,05 рад, модуль сдвига материала вала G = 0,8 1011Па, α=0,2м., b=0,4м., d=0.02м.

Решение. Решение задачи начинаем с определения опорных реактивных моментов. Отбросим опоры и заменим их действие на вал моментами Ма и Мв (рис.2.17, б). для определения двух реактивных моментов в данном случае можно составить только одно уравнение равновесия:

= М - ,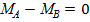

М_А + М_{В =} М.

Таким образом, задача один раз статически неопределима. Применяя метод сечений, выразим внутренние силовые факторы (крутящие моменты) на первом и втором участках через неизвестный пока реактивный момент М_А и момент М_В:

М = М_А , М = М_А – М.

Рассмотрим условие совместности деформаций двух участков (геометрическую сторону задачи).

Взаимный угол поворота сечений А и В равен нулю, так как оба сечения закреплены.

Т.е. = 0.

По формуле Гука (физическая сторона задачи):

где J_{Р –} полярный момент инерции сечения

Подставляя эти выражения в условие совместности деформации, получим:

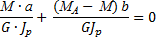
М_А ( 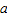+ b) = М b,

; .

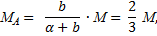
Эпюра крутящих моментов показана на рис.2.17, в.

Максимальные касательные напряжения, возникающие в поперечных сечениях, будут равны:

на первом участке: ,

на втором участке: .

Здесь - полярный момент сопротивления сечения.

Наибольшие напряжения возникают на первом участке, сравниваем их с допускаемыми

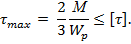
Из этого условия прочности находим момент М

Для расчета вала на жесткость построим эпюру углов закручивания:

при z = 0 = 0;

при Z = a ,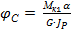

где ,

,

при Z = 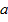+ b, = 0.

Эпюра 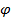показана на рис. 2.17, г.

Условие жесткости имеет вид:

,

отсюда .

Из двух значений момента М, полученных из расчетов на прочность и жесткость, за допускаемое значение принимаем меньшее, т.е. [М] = 188 Н .

Дата добавления: 2014-11-20