Статические моменты сечений

Геометрические характеристики плоских сечений

Прочность, жесткость и устойчивость элементов конструкции зависят от размеров и формы поперечных сечений этих элементов. В зависимости от вида нагружения в расчетные формулы входят различные геометрические характеристики сечений.

При изучении растяжения и сжатия стержня используется простейшая геометрическая характеристика – площадь сечения.

В расчетах на прочность и жесткость при кручении, изгибе, а также в расчетах сжатых стержней на устойчивость и ряде других случаев применяются более сложные геометрические характеристики сечений: статические моменты, осевые, полярные и центробежные моменты инерции, моменты сопротивления полярные и осевые.

Геометрические характеристики сечений простой формы определяются по формулам. Характеристики профилей стандартного проката (уголков, швеллеров, двутавров) приводятся в таблицах сортаметна прокатной стали.

Статическими моментами сечения (рис.3.1.) называются интегралы вида:

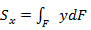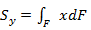, . (3.1.)

Каждый из этих интегралов представляет собой сумму произведений элементарных площадок dF на расстояние до соответствующей оси (х или y).

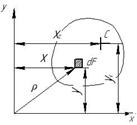
Рис.3.1.

Размерность статического момента – см³, м³.

В зависимости от положения оси, относительно которой вычисляется статический момент, он может быть положительным, отрицательным или равным нулю.

Для случаев, когда положение центра тяжести сечения известно, статические моменты определяются по формулам:

S_x = F y_C; S_y = F x _C. (3.2.)

Из формул (3.2.) следует, что статический момент относительно центральной оси равен нулю.

Если известны статические моменты сечения, то можно определить координаты его центра тяжести:

x _с = S_y / F; у _с = S_x/ F. (3.3)

Положение центра тяжести сложного сечения определяется в следующей последовательности:

1. Сложное сечение делится на простые фигуры;

2. Выбираются вспомогательные оси х, y;

3. Определяются площади и положения центров тяжести простых фигур в осях х,y;

4. По формулам (3.2.) вычисляются статические моменты каждой фигуры;

5. Положение центра тяжести всего сечения в осях х,y определяется по формулам:

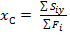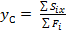; . (3.4.)

Пример 3.1. Определить положение центра тяжести сечения, представленного на рис.3.2.

Рис.3.2.

Решение. Разобьем сечение на два прямоугольника, как показано на рис.3.2.. выберем вспомогательную систему координат х и y. Определяем координаты центров тяжести каждого прямоугольника и их площади:

х ₁ = 1 см., y₁ = 5 cм., x ₂ = 4 см., y₂ = 1 см., F₁= 20 cм², F₂= 8 cм^2.

По формуле (3.2) находим статические моменты прямоугольников относительно осей х,y:

S_1х = F₁ y ₁ = 20 5 = 100 см³,

S_1y = F₁ x ₁ = 20 1 = 20 см³,

S_2х = F₂ y ₂ = 8 1 = 8 см³,

S_2y = F₂ x ₂ = 8 4 = 32 см³.

По формулам (3.4) вычисляем координаты центра тяжести всего сечения:

x _c =

y _c=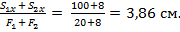

Дата добавления: 2014-11-20