Главные оси и главные моменты инерции

Изменение моментов инерции при повороте осей

Считаем, что заданы моменты инерции 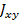_, , сечения относительно осей x,y.

Выберем новую систему координат x ₁y₁ c началом в той же точке O, но повернутую на угол α относительно первой. Угол α примем положительным при повороте исходной системы координат против хода часовой стрелки (рис.3.6).

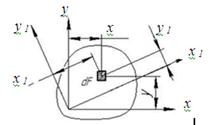
Рис.3.6.

Как видно из рисунка, координаты элемента dF выражаются через координаты xy следующим образом:

x ₁ = x cos 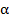+ y sin 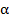; y₁ = y cos 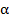– x sin 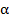. (3.22.а)

Подставив выражения (3.22,а) в интегралы (3.18) находим:

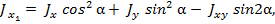(3.23)

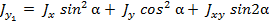_,(3.24)

. (3.25)

Складывая почленно выражения (3.23) и (3.24) получим

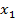J + J 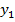= J _x + J _y = J_p. (3.26)

Таким образом, сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей остается постоянной при повороте осей на любой угол и равна полярному моменту инерции относительно начала координат.

Исследование зависимостей (3.23) и (3.24) на экстремум показывает, что существует такое положение двух взаимно перпендикулярных осей, при котором осевые моменты инерции принимают экстремальные значения, т.е. достигают максимума и минимума, причем для одной оси момент инерции максимален, для другой минимален.

Оси, относительно которых осевые моменты инерции экстремальны (максимальны и минимальны) называются главными осями. Моменты инерции относительно главных осей называются главными моментами инерции. Главные оси, проходящие через центр тяжести сечения называются главными центральными осями.

Чтобы найти значение угла α_о, определяющего положение главных осей, исследуем на экстремум зависимость (3.23). Для этого приравняем нулю первую производную по α от J :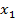

Отсюда

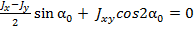. (3.27)

Сравнивая этот результат с выражением (3.25) приходим к заключению, что центробежный момент инерции относительно главных осей равен нулю.

Из (3.27) получим:

. (3.28)

Подставляя α₀ в формулы (3.23) и (3.24) найдем значения главных моментов инерции:

. (3.29)

В разделе 3.3. было отмечено, что относительно двух взаимно перпендикулярных осей, из которых хотя бы одна является осью симметрии, центробежный момент равен нулю. Следовательно, если сечение имеет ось симметрии, то это одна из главных центральных осей, вторая проходит через центр тяжести перпендикулярно первой.

Для сечений имеющих более двух осей симметрии, осевые моменты инерции относительно всех центральных осей являются главными и равны между собой (круг, квадрат, равносторонний треугольник и др.)

Пример 3.2. Для заданного сечения (рис.3.7) определить положение главных центральных осей и вычислить значения главных центральных моментов инерции.

Сечение составлено из швеллера №20 и листа сечением 220 х 10 мм.

Решение.

Выберем вспомогательные оси х,y. Выпишем координаты центров тяжести сечений швеллера С₁ и листа С₂ в этих осях и их площади.

Координаты центра тяжести швеллера:

x₁ = 2,07 см; y ₁ = 11см; площадь сечения F₁= 23,4 см³.

Размеры и другие геометрические характеристики швеллера находим по таблице сортамента.

Координаты центра тяжести листа: x ₂= 11см,

y₂ = 0,5см, площадь сечения F₂ = 22 х 1 = 22см².

Проведем центральные оси швеллера и листа .

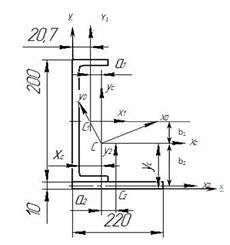
Рис.3.7.

По формулам 3.4 вычисляем координаты центра тяжести всего сечения:

,

.

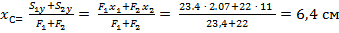Здесь S_1x = F₁ y ₁; S_2x = F₂ y₂; S_1y = F₁ x ₁; S_1y = F₂ x ₂ – статические моменты сечений швеллера и листа относительно осей х, y.

Через центр тяжести С всего сечения проведем оси x _с и y_c параллельно осям х,y.

Выпишем необходимые для дальнейшего расчета данные. Координаты центров тяжести сечений швеллера и листа в осях x _c и y _c:

а₁ = x₁- x₂ = 2.07 – 6.4 = -4, 33см;

b₁ = y₁- y₂ = 11-5, 91= 5,09 см;

а₂ = x₂- x_c = 11 – 6.4 = 4,6 см;

b₂ = y₂ – y_c = 0,5 – 5,91 = - 5, 41см.

Проверим правильность определения положения центра тяжести всего сечения. Для этого определим статические моменты сечения относительно осей х_с и y_c. Эти статические моменты при правильном определении координат х_с и y_c должны быть равны нулю.

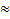S x _c = F₁b₁ + F₂b₂= 23,4 5,09 + 22 (-5,41) = 119,1 – 119,0 0;

Sy_c = F₁ а ₁ + F₂ а ₂= 23,4 (-4,33) + 22 4,6 = -101,3 + 101,2 .

Таким образом, координаты х_с и y_с центра тяжести всего сечения найдены правильно.

Моменты инерции сечения швеллера относительно собственных центральных осей х ₁и y ₁ (выписываем из таблицы сортамента):

J x ₁ = 1520 см⁴; J y ₁ = 113 см⁴.

Центробежный момент инерции J x₁y ₁ = 0

(так как ось х₁ - ось симметрии и поэтому оси х₁, y₁ – главные оси сечения швеллера).

Моменты инерции сечения листа определим по формулам (3.9) и (3.10)

,

,

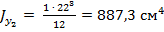J 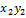= 0.

Вычислим моменты инерции всего сечения относительно осей х_с и y_с используя формулы перехода к параллельным осям (3.19) 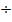(3.21)

J x _c = J + b₁²F₁+ J x ₂+ b₂²F₂ = 1520+ (5,09)² 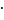23,4 + 1,83 + (-5,41) ² 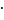22 = 2126 + 645,7 = 2772 (см⁴),

J y _c = J + a ₁²F₁+ J 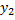+ a ₂²F₂ = 113+ (- 4,33)² 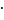23,4 + 887,3+ (4,6)² 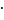22 = 551,7 + 1352,8 = 1905 (см⁴),

J _{X cYc} = J x ₁ y ₁+ a ₁ b₁F₁ + J x ₂ y ₂ + a ₂b₂ F₂ = 0 + (-4,33) 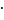5,09 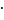23,4 + 0 + 4,6 (-5,41) 22 = -1063,2 (см⁴).

Определим угол наклона главных центральных осей к центральным осям х _с, y_c:

,

2α₀ = 67,8⁰; α₀ = 34⁰.

Положительный угол откладываем от оси х_с против хода часовой стрелке.

Величины главных центральных моментов инерции определяем по формуле (3.29)

,

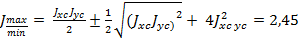2α₀= 67,8⁰; α₀= 34⁰.

Положительный угол откладываем от оси х_с против хода часовой стрелки.

Величины главных центральных моментов инерции определяем по формуле (3.29)

,

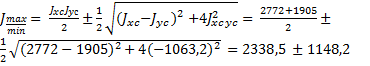J_max = 3487 см⁴; J_min= 1190 см⁴.

Для того, чтобы установить, относительно какой оси момент инерции максимален и относительно какой минимален, можно сопоставить значения моментов инерции J x _c и J y _c.

Поскольку J x _c J y _c., то J_max= J_xo и J_min= J_yo.

Проверка.

Центробежный момент инерции всего сечения относительно главных центральных осей должен равняться нулю.

По формуле (3.25) получаем:

.

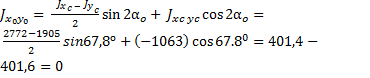Следовательно, вычисления выполнены верно.

Вопросы для самоконтроля

1. Назовите геометрические характеристики сечений, которые используются в расчетах на прочность и жесткость.

2. Как определяются геометрические характеристики профилей стандартного проката (уголков, швеллеров, двутавров)?

3. Что называется статическим моментом сечения относительно оси?

4. Какую размерность имеет статический момент?

5. Как определяется статический момент сечения?

6. Как определяются координаты центра тяжести простого и сложного сечения?

7. Чему равен статический момент сечения относительно центрально оси?

8. Что называется осевым, центробежным, полярным моментом инерции?

9. Какова размерность моментов инерции?

10. Какова зависимость между осевыми и полярным моментом инерции?

11. Какие знаки могут иметь моменты инерции?

12. Чему равны моменты инерции прямоугольного сечения относительно оси, совпадающей с одной из его сторон, и относительно центральной оси, параллельной одной из его сторон?

13. Чему равен момент инерции круга и кольца относительно центральной оси?

14. Чему равны полярные моменты инерции круга и кольца относительно их центров?

15. Чему равны моменты инерции треугольника относительно оси, проходящей через основание, и относительно центральной оси, параллельной основанию?

16. Как определяются моменты инерции сложного сечения?

17. Какова зависимость между осевыми и центробежными моментами для параллельных осей?

18. Как меняются осевые и центробежный моменты инерции при повороте осей?

19. Как меняется сумма моментов инерции относительно двух взаимно перпендикулярных осей при их повороте?

20. Какие оси называются главными осями и главными центральными осями инерции?

21. Чему равен центробежный момент инерции относительно главных осей?

22. Какова особенность главных моментов инерции?

23. В каких случаях без вычислений можно установить положение главных осей инерции?

24. По какой формуле определяется положение главных осей инерции?

25. По каким формулам определяются значения главных моментов инерции?

26. Какие оси являются главными центральными у сечений, имеющих более двух осей симметрии?

27. Какова последовательность определения значений главных центральных моментов инерции сложного сечения?

28. Как можно проверить правильность решения задачи по определению положения главных центральных осей инерции и моментов инерции относительно этих осей?

29. Как можно проверить правильность решения, задачи по определению координат центра тяжести сложного сечения?

Литература

1. Феодосьев, В.И. Сопротивление материалов [Текст]: Учеб. для вузов/ В.И.Феодосьев.- 10-е изд., перераб. и доп. - М.: Изд-во МГТУ им. Н.Э.Баумана, 2000. - 592 е.: ил.; 22 см. - 3000 экз. - ISBN 5-7038-1340-9.

2. Степин П.А. Сопротивление материалов [Текст]: Учебник 11-е изд., стер. - СПб.: изд. "Лань", 2010-320 е.: ил. - 1500 экз. - ISBN 978-5-8114-1038-5.

3. Кривошапко С.Н. Сопротивление материалов: Учебник для бакалавров - М: Изд-во Юрайт, 2012.-413с.: ил. - 1000 экз. ISBN 978-5-9916-1515-0.

4. Ахметзянов М.Х., Лазарев И.Б. Сопротивление материалов: учебник/ М.Х. Ахметзянов, И.Б. Лазарев. - 2-е изд., перераб. и доп. - М.: Изд-во Юрайт. 2011. - 300с.-1000 экз. ISBN 978-5-9916-1253-1.

5. Молотников В.Я. Курс сопротивления материалов: Учебное пособие. - СПб.: Изд-во "Лань", 2006. - 384 е.: ил. - 2000 экз. ISBN 5-8114-0649-5.

6. Сопротивление материалов: Лабораторный практикум. (Рекомендовано учебно- методическим объединением по образованию в области металлургии в качестве учебного пособия для студентов высших учебных заведений)/ Авдеев В.И., Кравченко О.Ф., Кравченко Н.В. Старый Оскол: ООО "ТНТ", 2007. - 108 с.

Для заметок

Для заметок

Дата добавления: 2014-11-20