Расчет цилиндрических винтовых пружин

Цилиндрические винтовые пружины являются распространенными конструктивными элементами современных механизмов и машин. При проектировании пружин проводятся расчеты на прочность и жесткость.

Рассмотрим расчеты только цилиндрических винтовых пружин растяжения или сжатия, изготовленных из проволоки круглого поперечного сечения.

а) б)

Рис.2.18

Пружина характеризуется следующими геометрическими параметрами (Рис.2.18,а): диаметр витка D; диаметр сечения проволоки d, из которой навита пружина; число рабочих витков n (концевые витки, служащие для крепления пружины к смежным деталям, не учитываются); шаг витка пружины h.

Ограничимся рассмотрением винтовой пружины с малым шагом витков h по сравнению с диаметром пружины D. При этом условии наклоном витков можно пренебречь и считать, что любое поперечное сечение проволоки параллельно силам Р, растягивающим пружину.

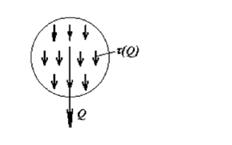
Для определения внутренних силовых факторов, возникающих в сечении пружины, рассечем один из витков плоскостью, проходящей через ось пружины, и рассмотрим равновесие одной из отсеченных частей, например, верхней (Рис. 2.18, б).

а) б)

Рис.2.19

Учитывая, что угол наклона витка пружины мал, можно пренебречь наличием в сечении продольной силы и изгибающего момента, тогда из условия равновесия найдем, что в сечении должны возникать поперечная сила Q и крутящий момент М_К, равные:

Q = P; М_К = РD / 2. (2.41)

Оба эти силовых фактора вызывают только касательные напряжения.

Предполагая равномерное распределение напряжений от силы Q (рис.2.19, а) получим для любой точки сечения:

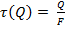, (2.42)

где - площадь сечения проволоки.

От крутящего момента напряжения распределены вдоль радиуса сечения по линейному закону, максимальные из которых достигаются на поверхности сечения (рис.2.19,б) и равны:

) = , (2.43)

здесь 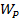= / 16 - полярный момент сопротивления сечения.

Таким образом, в наиболее опасном состоянии находится точка, расположенная на внутренней стороне сечения, где рассмотренные выше напряжения совпадают по направлению и суммируются:

. (2.44)

Если пружина навита из относительно тонкой проволоки по сравнению с ее диаметром

(d/2D ), то выражение (2.44) для максимальных напряжений упрощается:

. (2.45)

При отклонении конструкции пружины от сделанного допущения о малости шага витка прибегают к иной формуле:

, (2.46)

где поправочный коэффициент , учитывающий кривизну витка и влияние прочих внутренних силовых факторов, может быть определен по эмпирической формуле:

. (2.47)

Выраженной через индекс пружины с = D/d.

Осевое перемещение (осадка) пружины может быть подсчитано только с учетом деформации кручения, так как деформации от остальных силовых факторов малы.

С учетом сказанного перемещение пружины равно:

, (2.48)

где G- модуль сдвига материала.

Следует отметить, что осевое перемещение пружины во много раз больше деформации стержня, из которого она навита, нагруженного по оси той же силой Р.

Это свойство пружины объясняет их высокую амортизирующую способность.

Зависимость осевого перемещения от усилия 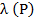часто называют характеристикой пружины.

Выразим ее в следующем виде:

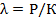. (2.49)

Величину К в последнем выражении называют жесткостью пружины:

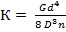, (2.50)

которая показывает величину усилия, вызывающего перемещение, равно единице, и имеет размерность Н/м.

Дата добавления: 2014-11-20