Моменты инерции сечения

Осевыми (или экваториальными) моментами инерции сечения называются интегралы:

, , (3.5.)

где х,y – координаты элементарной площадки dF в системе координат хОy (см.рис.3.1).

Интеграл (3.6.)

называется центробежным моментом инерции.

В разделе кручение уже встречался интеграл вида

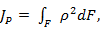(3.7)который называется полярным моментом инерции.

Как видно из рис.3.1.

Поэтому (3.8)

Моменты инерции имеют размерность м⁴ (или см⁴). Осевые и полярный моменты инерции только положительны. Центробежный момент инерции может быть положительным, отрицательным или равным нулю. Вычислим моменты инерции для сечений простой формы.

Прямоугольник (рис.3.3).

Рис.3.3.

Выделим элемент площади dF на расстоянии y от оси х в виде полосы шириной b и высотой dy.

Получим . (3.9)

Аналогично найдем 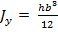. (3.10)

Осевые и центробежные моменты инерции относительно осей x ₁, y ₁ равны:

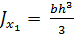, (3.11)

, (3.12)

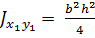. (3.13)

Треугольник (рис.3.4.).

Осевой момент инерции треугольника относительно оси, проходящей через его центр тяжести параллельно основанию равен:

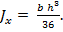(3.14)

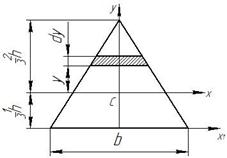
Рис.3.4.

Осевой момент инерции относительно оси Х_1, проходящей по основанию равен:

. (3.15)

Круг.

Осевой момент инерции круга относительно любой оси, проходящей через его центр тяжести, равен:

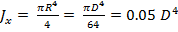. (3.16)

Полярный момент инерции круга относительно его центра J_P находится по формуле (2.14).

Очевидно, .

Осевой момент инерции сечения, имеющего форму кругового кольца с наружным диаметром D и внутренним D₀, можно определить как разность между соответствующими моментами инерции наружного и внутреннего кругов:

. (3.17)

При вычислении моментов инерции сложного сечения разбивают сечение на простые части, моменты инерции которых известны. Момент инерции сечения равен сумме моментов инерции его составных частей.

Отметим, что моменты инерции прокатных профилей приводятся в таблицах сортамента прокатной стали.

Дата добавления: 2014-11-20