Показатели вариации

ВАРИАЦИЯ ПРИЗНАКА

Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но не раскрывает расположение вариант изучаемого признака относительно центра распределения.

Средняя величина признака в двух разных совокупностях может быть одинаковой, но в одном случае варианты отличаются от нее незначительно (вариация — мала), а в другом случае — значительно (вариация — велика).

Степень вариации имеет значение для характеристики надежности средней величины. Если индивидуальные значения признака мало отличаются друг от друга, то средняя будет достаточно показательной характеристикой свойств данной совокупности. Если ряд распределения характеризуется значительным рассеиванием индивидуальных значений (вариант), то средняя будет не надежной характеристикой изучаемой совокупности и ее практическое применение будет ограничено.

Для измерения вариации (колеблемости) признака в статистике применяются различные абсолютные и относительные показатели:

1. Размах вариации.

2. Среднее линейное отклонение.

3. Относительное среднее линейное отклонение.

4. Дисперсия.

5. Коэффициент вариации.

Относительными показателями вариации являются коэффициент вариации и относительное среднее линейное отклонение, остальные из перечисленных показателей — абсолютные величины.

Размах вариации определяется как разность между максимальным и минимальным значением изучаемого признака:

(5.1)

Размах вариации является самым простым показателем колеблемости признака. Недостаток его состоит в том, что он показывает отклонение только крайних значений признака и не дает обобщенной характеристики вариации.

Среднее линейное отклонение определяется как средняя арифметическая абсолютных отклонений индивидуальных значений признака от среднего уровня этого признака/

Для несгруппированных данных

. (5.2)

Для сгруппированных данных

. (5.3)

Заметим, что в числителе формул (5.2) и (5.3) представлены суммы абсолютных отклонений без учета знака. Если разности суммировать с учетом знака, числитель этих формул всегда будет равен нулю.

Относительное среднее линейное отклонение определятся как отношение среднего линейного отклонения к средней арифметической, и выражается в процентах:

. (5.4)

Дисперсия представляет собой среднюю арифметическую из квадратов отклонений индивидуальных значений признака от среднего уровня.

Для несгруппированных данных дисперсия определяется по формуле

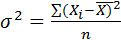. (5.5)

Для сгруппированных данных

. (5.6)

Среднее квадратическое отклонение — квадратный корень из дисперсии.

Для несгруппированных данных

. (5.7)

Для сгруппированных данных

. (5.8)

Этот показатель является мерой надежности средней: чем меньше среднее квадратическое отклонение, тем точнее средняя арифметическая отражает средний уровень признака.

Коэффициент вариации определяется по формуле

. (5.9)

Этот показатель служит относительным измерителем колеблемости признака и однородности совокупности. Если его значение превышает 33%, то совокупность квалифицируют как недостаточно однородную.

Дисперсия и среднее квадратическое отклонение являются наиболее широко применяемыми показателями вариации. Это связано с тем, что они относятся к числу основополагающих показателей теории вероятности и математической статистики, служащих фундаментом теории статистики.

В экономических исследованиях среднее квадратическое отклонение часто используется при определении уровня различных рисков.

Пример. По данным таблицы 5.1 оценим уровень колеблемости стажа рабочих цеха.

Таблица 5.1 – Распределение рабочих цеха по стажу

№	Стаж рабочего	Количество рабочих	Расчетные величины
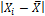
				1,7	5,1	2,89	8,67
				0,7	2,8	0,49	1,96
				0,3	1,5	0,09	0,45
				1,3	3,9	1,69	5,07
				2,3	2,3	5,29	5,29
Итого			х	15,6	х	21,44

1. Размах вариации:

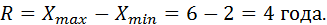
2. Среднее линейное отклонение:

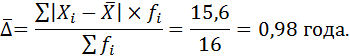
3. Относительное среднее линейное отклонение:

=

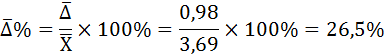
4. Дисперсия:

5. Среднее квадратическое отклонение:

6. Коэффициент вариации.

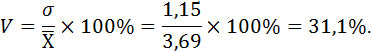
Дата добавления: 2014-11-08