Основная тенденция развития в рядах динамики

Важным направлением в исследовании закономерностей социально-экономических процессов является изучение основной тенденции развития (тренда).

Выявление основной тенденции развития в статистике называют так же выравниваем временного ряда, а методы выявления основной тенденции — методами выравнивания.

Задача состоит в том, чтобы выявить общую тенденцию развития явления, элиминированную от влияния различных случайных факторов.

Для решения этой задачи в статистике применяются различные приемы:

1) графическое изображение с применением линейной диаграммы;

2) укрупнение интервалов;

3) построение скользящей средней;

4) аналитическое выравнивание.

Метод укрупнения интервалов состоит в преобразовании первоначального ряда динамики в ряд с более продолжительным периодом (месячный — в квартальный, квартальный — в годовой и т.д.).

После укрупнения интервалов основная тенденция динамики может проявиться более четко. Но такой прием значительно сокращает длину динамического ряда, что затрудняет анализ.

Данного недостатка лишен метод скользящей средней, суть которого состоит в следующем.

Формируется новый динамический ряд, уровни которого рассчитываются как средняя арифметическая из некоторого числа уровней первоначального ряда, начиная с первого. Затем такой же расчет делается для следующей группы уровней первоначального ряда, начиная с его второго уровня и так далее. Полученные средние соотносятся с серединой укрупненных интервалов. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один уровень.

При расчете скользящей средней технически удобнее укрупненный интервал строить из нечетного числа уровней первоначального ряда. Расчет по четному числу этих уровней создает неудобство, так как рассчитанную среднюю приходится соотносить с точкой, являющейся серединой расстояния между двумя интервалами.

Результаты расчета скользящей средней приведены в таблице 6.2, а ее графическое изображение представлено на рис. 6.1.

Таблица 6.2 – Динамика добычи угля

Показатель	День,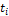
Добыча угля, тонн (первоначальный ряд),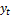
Скользящая средняя (трехдневная),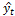

Расчет уровней 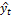, скользящей средней, представленных в таблице 6.2, производится следующим образом:

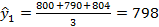
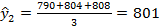
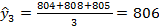и т.д.

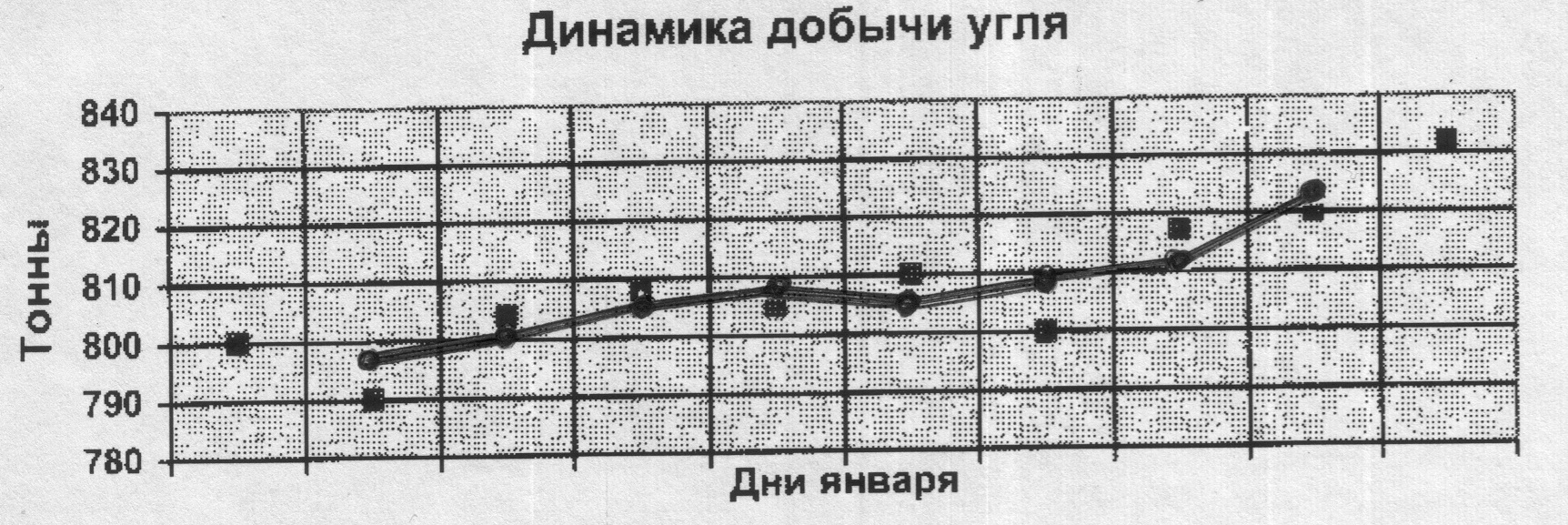
Рис. 6.1 – Результаты обработки данных методом скользящей средней

На графике точками показаны первоначальные данные, а ломаной — данные, сглаженные по трем дням.

Укрупнение интервалов и метод скользящей средней позволяют выявить общую тенденцию развития явления, но получить обобщенную статистическую модель тренда с помощью этих методов невозможно.

Для решения этой задачи используется аналитическое выравнивание ряда динамики. В этом случае общая тенденция изучаемого явления рассчитывается как функция времени.

Выбор формы кривой (вида функции) основывается на содержательном анализе изучаемого явления, на результатах предыдущих исследований в данной области, а также на оценке графического изображения ряда динамики в форме линейной диаграммы, построенной по первичной информации, по укрупненным интервалам или с помощью метода скользящей средней.

Чаще всего целесообразно применять прямую линию, реже – параболу 2-го порядка, логарифмическую или показательную функции.

После обоснования и выбора функции для выявления общей тенденции развития анализируемого явления, определяются ее параметры. Задача решается на основе метода наименьших квадратов.

Суть метода наименьших квадратов состоит в требовании минимизации суммы квадратов отклонений фактических значений уровней динамического ряда от их значений, вычисленных по функции выравнивания:

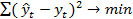(6.12)

Математически эта задача решается следующим образом. Первые производные выражения (6.12) приравниваются к нулю, что дает систему уравнений, в которых неизвестными являются параметры функции, выбранной для сглаживания динамического ряда.

Система уравнений зависит от вида функции, выбранной для выравнивания динамического ряда.

Дата добавления: 2014-11-08