Закон сохранения момента импульса. В замкнутой системе вращающихся тел выполняется закон сохранения момента импульса: «Изменение момента импульса вращающихся тел в замкнутой системе равен нулю

В замкнутой системе вращающихся тел выполняется закон сохранения момента импульса: «Изменение момента импульса вращающихся тел в замкнутой системе равен нулю, то есть или 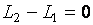», где – векторная сумма моментов импульса тел до взаимодействия; – векторная сумма моментов импульса тел после взаимодействия. Кинетическая энергия вращающегося тела

Поступательно движущееся тело обладает кинетической энергией

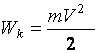, (1.14)

где m – масса тела или мера инертности поступательно движущегося тела, – квадрат его линейной скорости.Движение вращающегося тела характеризуется угловой скоростью , а мерой его инертности является момент инерции J. Связь линейной и угловой скоростей 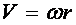. Записав формулу (1.14) для i -й точки, вращающейся вокруг оси ОО, получим

, где 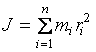– момент инерции всех точек тела.Следовательно, ,

то есть кинетическая энергия вращающегося тела равна той работе, которую может совершить это тело до полной остановки. 1.5. Работа и мощность вращающихся тел

За время вращающееся тело совершит работу 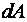, равную произведению момента силы M на угол поворота 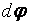, сделанный радиусом этого тела, то есть

.

Работу, совершенную вращающимся телом за единицу времени, называют мощностью вращающегося тела N, то есть

, ,

где 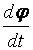– мгновенное значение угловой скорости .

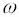Поэтому:

Отдельные точки вращающегося тела имеют различные линейные скорости 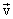. Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости 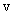определяется скоростью вращения тела 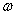и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени 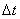тело повернулось на угол 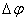(рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный

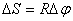
Линейная скорость точки по определению.

Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение:

подставляя значение скорости из(1), находим:

Тангенциальное ускорение

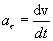
Воспользовавшись тем же отношением получаем

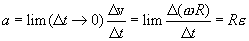
Таким образом, как нормальное, так и, тангенциальное ускорения растут линейно с расстоянием точки от оси вращения.

6. Зако́ны Ньюто́на — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год).

Дата добавления: 2014-11-08