В чем состоит закон сохранения механической энергии?

7.

Механическая система. Закон сохранения импульса механической системы.

Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.

Материальное абсолютно твердое тело мы также будем рассматривать как систему материальных точек, образующих это тело и связанных между собой так, что расстояния между ними не изменяются, все время остаются постоянными.

Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п. (т.е. различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.

Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.

В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.

Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом - 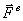, а внутренние - .

Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.

Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.

Активными или задаваемыми силами называются все остальные силы, все кроме реакций.

Необходимость этой классификации сил выяснится в следующих главах.

Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем. Например, если рассматривать движение всей солнечной системы в целом, то сила притяжения Земли к Солнцу будет внутренней; при изучении же движения Земли по её орбите вокруг Солнца та же сила будет рассматриваться как внешняя.

Закон сохранения импульса формулируется так: если сумма внешних сил равна нулю, то импульс системы тел сохраняется. Иначе говоря, в этом слу­чае тела могут только обмениваться импульсами, суммар­ное же значение импульса не изменяется.

Импульс, очевидно, сохраняется в изолированной сис­теме тел, так как в этой системе на тела вообще не дейст­вуют внешние силы. Но область применения закона сохра­нения импульса шире: если даже на тела системы действуют внешние силы, но их сумма равна нулю (т. е. система является замкнутой), то импульс системы все равно сохраняется.

Полученный результат справедлив для системы, содер­жащей произвольное число тел:

, (9)

где , … — скорости тел в начальный момент времени; 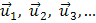— скорости тел в конечный момент.

Так как импульс — векторная величина, то уравне­ние (9) представляет собой компактную запись трех уравнений для проекций импульсов системы на оси коор­динат.

Если сумма внешних сил не равна нулю, но сумма про­екций сил на какое-то направление равна нулю, то проек­ция суммарного импульса системы на это направление не меняется. Например, систему тел на Земле или вблизи по­верхности Земли нельзя считать изолированной, так как на тела действует внешняя сила — сила тяжести. Однако вдоль горизонтального направления сила тяжести не дей­ствует и сумма проекций импульсов тел на это направле­ние будет оставаться неизменной, если действием сил тре­ния можно пренебречь.

В изолированной системе тел импульс системы сохра­няется. Также он может сохраняться в случае, если сумма внешних сил, действующих на систему, равна нулю.

8. Работа силы. Элементарная работа. Мощность. Силы консервативные и неконсервативные.

Определение работы. Второй закон Ньютона в форме 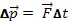позволяет определить, как меняется скорость тела по модулю и направлению, если на него в течение времени ∆ t действует сила .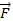

Во многих случаях важно уметь вычислять изменение скорости по модулю, если при перемещении тела на на него действует сила 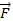.Воздействия на тела сил, приводя­щих к изменению модуля их скорости, характеризуются величиной, зависящей как от сил, так и от перемещений тел. Эту величину в механике и называют работой силы

Элементарная работа силы равна скалярному произведению силы на элементарное перемещение или на дифференциал радиуса вектора точки приложения силы.

Элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки.

Если сила задана своими проекциями (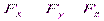) на оси координат и элементарное перемещение задано своими проекциями () на оси координат, то элементарная работа силы равна:
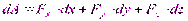(аналитическое выражение элементарной работы).
Работа силы на любом конечном перемещении 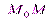равна взятому вдоль этого перемещения интегралу от элементарной работы.

Мощностью силы называется величина, определяющая работу, совершаемую силой в единицу времени. В общем случае мощность равна первой производной по времени от работы.
,
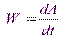Мощность равна скалярному произведению силы на скорость.

Единицей измерения мощности в СИ является –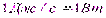

В технике за единицу силы принимается .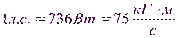

Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное.

Характерное свойство таких сил – работа на замкнутой траектории равна нулю:

К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.

Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное.

Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.

9,. Кинетическая энергия. Потенциальная энергия. Закон сохранения полной механической энергии.

Кинетической энергией называется энергия, связанная с движением точки и зависящая от ее скорости. Скорость тела изменяется под действием результирующей силы F.

, где m - масса тела, V - скорость тела.
Кинетическая энергия системы точек определяется как сумма кинетических энергий всех точек системы. Изменение кинетической энергии системы равно работе всех сил, действующих на ее точки.

Потенциальная энергия — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в полеконсервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в Международной системе единиц (СИ) является джоуль.

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными (потенциальными).

Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.

Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.

Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системыможет быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.

С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимостью законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.

В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Говорят, что возможен переход энергии одного типа в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Ввиду условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно.

Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первое начало термодинамики, а в электродинамике — теорема Пойнтинга.

С математической точки зрения закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени. 1. Что такое полная механическая энергия?

1. Сумму кинетической и потенциальной энергии тел в какой-то момент времени называют полной механической энергией.

2. Закон сохранения механической энергии состоит в том, что полная механическая энергия замкнутой системы остается неизменной.

Дата добавления: 2014-11-08