Физический смысл

Акустическое число Рейнольдса

В акустике пользуются числом Рейнольдса для количественной характеристики соотношения нелинейных и диссипативных членов в уравнении, описывающем распространение волны конечной амплитуды. В этом случае число Рейнольдса принимает следующий вид:

Rea= ρc 0 Vωb,

где

· ρ — плотность среды, кг/м³;

· V — характерный масштаб колебательной скорости;

· ω — круговая частота;

· c 0 — скорость звука в среде;

· b — параметр диссипации.

Число Рейнольдса есть мера отношения сил инерции, действующих в потоке, к силам вязкости. Плотность в числителе выражения Re= ρvD Γ η = vD Γ ν характеризует инерцию частиц, отклонившихся от движения по прямой, а вязкость в знаменателе показывает склонность жидкости препятствовать такому отклонению.

Если у потока число Рейнолдса достаточно большое (выше критической величины), то жидкость можно рассматривать как идеальную. В таком случае вязкостью можно пренебречь.

16. Всякая реальная жидкость обладает вязкостью, т.е. свойством оказывать сопротивление при перемещении одной части жидкости относительно другой.

Это свойство проявляется в двух случаях:

1. при движении тела в жидкости;

2. при движении жидкости относительно тела.

В первом случае сила сопротивления жидкости движению тела (например, сила сопротивления воды движению подводной лодки) характеризуется динамической вязкостью. Если же жидкость движется относительно твердого тела (например, течение воды, бензина, нефти в трубопроводе или крови в артериях и венах), то силу сопротивления движению, возникающая между двумя слоями жидкости, лучше характеризовать кинематической вязкостью.

В отличие от газов (где расстояния между молекулами большое и сила внутреннего трения определяется в основном переносом количества движения (импульса) между слоями газа) в жидкостях, где расстояния между молекулами много меньше, вязкость обусловлена в первую очередь молекулярным взаимодействием, ограничивающим подвижность молекул. В жидкости молекула может проникнуть в соседний слой лишь при образовании в нем полости, достаточной для перескакивания туда молекулы. На образование полости (на "рыхление" жидкости) расходуется так называемая энергия активации вязкого течения. Энергия активации уменьшается с ростом температуры Т и понижением давления Р. В этом состоит одна из причин резкого снижения вязкости жидкостей с повышением температуры и роста ее при высоких давлениях. При образовании полости внутренняя энергия жидкости увеличивается (нагревается). Это происходит только тогда, когда жидкость движется, т.е. на жидкость действуют внешние силы. Это означает, что из-за наличия сил внутреннего трения кинетическая энергия движения жидкости превращается в ее внутреннюю энергию. Очевидно, что чем меньше кинетической энергии жидкости превращается в ее внутреннюю энергию, тем меньше роль вязкости. Но кинетическая энергия некоторого количества жидкости пропорциональна ее плотности 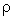, а работа сил внутреннего трения пропорциональна динамической вязкости 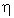. Поэтому относительное влияние вязкости на движение жидкости относительно твердого тела определяется величиной

,

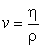
(1)

которую и называют кинетической вязкостью жидкости.

Величина v точнее, чем величина 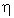характеризует роль вязкости при прочих равных условиях. Учитывая, что величины 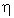и v можно определить не только для жидкости, но и для газа, рассмотрим следующий пример. При температуре около 0⁰С величина 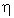для воды примерно в 100 раз больше, чем для воздуха. Это означает, что сила сопротивления, которая возникает при движении твердого тела в воде, будет значительно больше, чем при движении этого же тела в воздухе. При тех же условиях кинематическая вязкость v воды почти в 10 раз меньше кинематической вязкости воздуха, а это означает, что сила сопротивления, возникающая при протекании воды через трубу диаметром d, будет гораздо меньше, чем при протекании через эту трубу воздуха.

Силы сопротивления, возникающие при движении жидкости в трубе, зависят не только от вязкости жидкости, но и от характера ее движения. Течение жидкости называется стационарным, если вектор скорости частиц жидкости в каждой точке пространства, занятого текущей жидкостью, остается постоянным. Другими словами, любая частица жидкости проходит данную точку пространства с одной и ой же по величине и направлению скоростью. При стационарном течении жидкость движется как бы слоями, причем каждый слой скользит относительно соседнего без перемешивания, а векторы скорости всех частиц жидкости параллельны оси трубы. Такое течение жидкости называется ламинарным (слоистым). При увеличении скорости течения жидкости слоистый характер движения жидкости нарушается, и ламинарное течение переходит в турбулентное, при котором силы сопротивления движению жидкости в трубе резко возрастают. Определить, какой вид движения жидкости будет в данной трубе, можно с помощью экспериментально установленного критерия, который называется числом Рейнольдса:

,

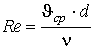
(2)

где J _ср - средняя скорость потока жидкости; d - диаметр трубы; 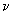- кинематическая вязкость жидкости. Число Re - величина безразмерная. Если Re < 1000, то течение в трубе будет ламинарным, если Re > 2000 - течение турбулентное. При значении Re между 1000 и 2000 течение жидкости нестабильное и может изменяться случайным образом.

В данной работе определение кинематической вязкости растворов спирта производится через измерение времени вытекания жидкости из капиллярного вискозиметра под действием силы тяжести. Ламинарность движения жидкости в вискозиметре обеспечивается небольшой разностью давлений на концах капиллярной трубки и малым ее диаметром.

Рассмотрим движение жидкости (рис. 1) по капилляру длиной 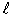под действием разности давлени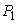й и 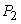в верхнем и нижнем концах трубки. При ламинарном течении жидкости (например, воды) скорость направленного движения всех частиц, находящихся на одинаковом расстоянии от оси, будет одинакова.

Из-за наличия внутреннего трения наибольшей скоростью будет обладать центральная часть жидкости, наименьшей скоростью, равной нулю, часть жидкости, соприкасающаяся со стенкой трубки. Средняя же скорость слоев жидкости определяется законом Пуазейля

,

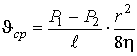
(3)

где 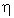- динамическая вязкость жидкости.

За время 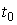через трубку протечет объем воды, равный

,

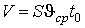
(4)

где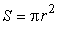

-

поперечное сечение капилляра. Подставим в (4) значение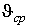

из (3)

,

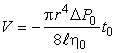
(5)

где 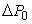- разность давлений на концах трубки; 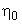- динамическая вязкость воды. Выражение (5) есть формула Пуазейля, определяющая объем жидкости, протекающей через капилляр за время 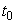. Зальем в вискозиметр раствор спирта. Такой же объем раствора спирта пройдет через капилляр за время 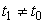, так как

.

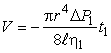
(6)

Учитывая, что 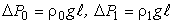получим

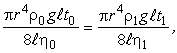
(7)

или

.

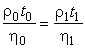
(8)

С учетом (1) окончательно имеем

,

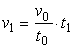
(9)

где 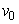и 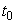- кинематическая вязкость и время протекания стандартной (эталонной) жидкости через капилляр. Следовательно, из (9), зная кинематическую вязкость эталонной жидкости 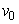, время ее прохождения через капилляр 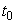и время прохождения 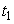через капилляр такого же объема исследуемой жидкости, можно определить кинематическую вязкость последней.

Дата добавления: 2014-11-08