
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Термодинамическое определение
|
|
|
|
Исходя из определения идеального газа, в нем отсутствует потенциальная составляющая внутренней энергии (отсутствуют силы взаимодействия молекул, кроме ударного). Таким образом, внутренняя энергия идеального газа представляет собой только кинетическую энергию движения его молекул. Ранее (уравнение 2.10) было показано, что кинетическая энергия поступательного движения молекул газа прямо пропорциональна его абсолютной температуре
Основное уравнения модели идеального газа
Основное уравнение молекулярно-кинетической теории идеального газа утверждает:
Произведение давления идеального газа на его объем пропорционально плотности числа молекул в газе и средней кинетической энергии поступательного движения отдельной молекулы,т.е.
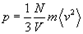
Внутренняя энергия идеального газа.
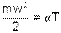
|
Используя выражение универсальной газовой постоянной (4.6), можно определить величину константы α
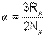
|
Таким образом, кинетическая энергия поступательного движения одной молекулы идеального газа будет определяться выражением
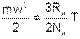
| (4.10) |
В соответствии с кинетической теорией, распределение энергии по степеням свободы равномерное. У поступательного движения 3 степени свободы. Следовательно, на одну степень свободы движения молекулы газа будет приходиться 1/3 ее кинетической энергии
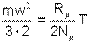
| (4.11) |
Для двух, трех и многоатомных молекул газа кроме степеней свободы поступательного движения есть степени свободы вращательного движения молекулы. Для двухатомных молекул газа число степеней свободы вращательного движения равно 2, для трех и многоатомных молекул - 3.
Поскольку распределение энергии движения молекулы по всем степеням свободы равномерное, а число молекул в одном киломоле газа равняется Nμ, внутреннюю энергию одного киломоля идеального газа можно получить, умножив выражение (4.11) на число молекул в одном киломоле и на число степеней свободы движения молекулы данного газа
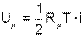
| (4.12) |
где Uμ - внутренняя энергия киломоля газа в Дж/кмоль,
i - число степеней свободы движения молекулы газа.
Для 1-атомного газа i = 3, для 2-атомного газа i = 5, для 3-атомного и многоатомного газов i = 6 (рис. 4.1)
Для многоатомного газа i=6, так как существуют 3 степени свободы поступательного движения и 3 степени свободы вращательного движения молекул. Может быть еще колебательное движение атомов в молекуле, но его обычно учитывают для реальных газов, используя экспериментальные данные. Для идеальных газов колебательное движение атомов в молекулах тоже может быть учтено при расчете внутренней энергии, об этом будет сказано в разделе "Зависимость теплоемкостей идеальных газов от температуры". На данном этапе изложения материала будем руководствоваться молекулярно-кинетической теорией идеального газа. В соответствии с ней атомы в молекулах идеального газа имеют жесткие связи, т.е. колебательного движения атомов в молекулах нет.
Для одного килограмма идеального газа удельная внутренняя энергия в Дж/кг определяется делением выражения (4.12) на молярную массу газа
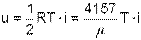
| (4.13) |
произвольного количества газа внутренняя энергия определяется как произведение его массы на удельную внутреннюю энергию этого газа

| (4.14) |
где m - масса газа в кг,
U - полная внутренняя энергия идеального газа.
Если система состоит из нескольких различных по физическим свойствам газов, то, подчиняясь закону сложения (аддитивности), его полная внутренняя энергия будет определяться суммой внутренних энергий компонентов газовой смеси

| (4.15) |
где n - число компонентов газа в системе.
Полученные уравнения внутренней энергии идеального газа (4.12) - (4.15) указывают на то, что внутренняя энергия идеального газа зависит только от абсолютной температуры газа и числа степеней свободы движения его молекул
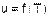
|
или
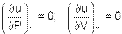 Согласно закону Джоуля, выведенному эмпирически, внутренняя энергия идеального газа не зависит от давления или объёма. Исходя из этого факта, можно получить выражение для изменения внутренней энергии идеального газа. По определениюмолярной теплоёмкости при постоянном объёме, (∂ U ∂ T) V = CV. Так как внутренняя энергия идеального газа является функцией только от температуры, то
Δ U =∫ T 2 T 1 νCV d T.
Эта же формула верна и для вычисления изменения внутренней энергии любого тела, но только в процессах при постоянном объёме (изохорных процессах); в общем случае CV (T, V) является функцией и температуры, и объёма.
Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим:
Δ U = νCV Δ T,
где ν — количество вещества, Δ T — изменение температуры.
Для идеального газа внутренняя энергия равна:
U = i 2⋅ νRT,
где i - количество степеней свободы, R - универсальная газовая постоянная.
Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
p ⋅ VM = R ⋅ T,
где
· p — давление,
· VM — молярный объём,
· R — универсальная газовая постоянная
· T — абсолютная температура, К.
Так как VM = Vν, где ν — количество вещества, а ν = mM, где m — масса, M — молярная масса, уравнение состояния можно записать:
p ⋅ V = mMR ⋅ T.
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.
Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную r, значение которой необходимо было измерять для каждого газа:
p ⋅ V = r ⋅ T,
Менделеев же обнаружил, что r прямо пропорциональна ν, коэффициент пропорциональности R он назвал универсальной газовой постоянной.
Связь с другими законами состояния идеального газа[править | править вики-текст]
В случае постоянной массы газа уравнение можно записать в виде:
p ⋅ VT = ν ⋅ R,
p ⋅ VT =const.
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
T =const⇒ p ⋅ V =const — закон Бойля — Мариотта.
p =const⇒ VT =const — Закон Гей-Люссака.
V =const⇒ pT =const — закон Шарля (второй закон Гей-Люссака, 1808 г.)
А в форме пропорции p 1⋅ V 1 T 1= p 2⋅ V 2 T 2 этот закон удобен для расчёта перевода газа из одного состояния в другое.
С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
H2+Cl2=2HCl.
1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
N2+3H2=2NH3.
T =const⇒ p ⋅ V =const — закон Бойля — Мариотта.
Закон Бойля — Мариотта назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
p =(γ −1) ρε,
где γ — показатель адиабаты, ε — внутренняя энергия единицы массы вещества.
Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. И это обстоятельство может быть прояснено на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.
С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение P ⋅ V немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение P ⋅ V увеличивается.
Молекулярно-кинетическая теория (сокращённо МКТ) — теория, возникшая в XIX веке и рассматривающая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:
· все тела состоят из частиц: атомов, молекул и ионов;
· частицы находятся в непрерывном хаотическом движении (тепловом);
· частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.
МКТ стала одной из самых успешных физических теорий и была подтверждена целым рядом опытных фактов. Основными доказательствами положений МКТ стали:
· Диффузия
· Броуновское движение
· Изменение агрегатных состояний вещества
На основе МКТ развит целый ряд разделов современной физики, в частности, физическая кинетика и статистическая механика. В этих разделах физики изучаются не только молекулярные (атомные или ионные) системы, находящиеся не только в «тепловом» движении, и взаимодействующие не только через абсолютно упругие столкновения. Термин же молекулярно-кинетическая теория в современной теоретической физике уже практически не используется, хотя он встречается в учебниках по курсу общей физики.
p =13 m 0 nv 2. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения).
Упрощенный вывод основного уравнения МКТ
Пусть имеется N частиц массой m 0 в некотором кубическом сосуде.
Так как молекулы движутся хаотически, то события, состоящие в движении в одном из шести независимых направлений пространства, совпадающих с осями декартовой системы координат, равновероятны.
Поэтому, в каждом из этих направлении движется 16 N частиц.
Пусть все частицы обладают одинаковой скоростью v.
Каждая из частиц, сталкивающихся со стенкой, передаёт ей импульс Δ P =2 m 0 v.
Если площадь стенки S, а концентрация - n, то количество частиц, сталкивающихся со стенкой за время Δ t равно N =16 nS Δ tv.
Так как p = FS, а F =Δ P Δ tN - суммарная сила взаимодействия частиц со стенкой, то подставив соответствующие значения получим p =13 m 0 nv 2,
так как Ek ¯=12 mv 2¯, то p =23 nEk ¯
Уравнение среднеквадратичной скорости молекулы
Уравнение среднеквадратичной скорости молекулы легко выводится из основного уравнения МКТ для одного моля газа.
Ek =12 mv 2¯=32 kT,
Nam = Mr, где Mr — молярная масса газа, m — масса молекулы газа.
Отсюда окончательно
v ¯=√3 kTNA, √3 RT
Mr Mr
- основное уравнение МКТ идеального газа. Выведено в предположении, что давление газа есть результат ударов его молекул о стенки сосуда.
Согласно закону Джоуля, выведенному эмпирически, внутренняя энергия идеального газа не зависит от давления или объёма. Исходя из этого факта, можно получить выражение для изменения внутренней энергии идеального газа. По определениюмолярной теплоёмкости при постоянном объёме, (∂ U ∂ T) V = CV. Так как внутренняя энергия идеального газа является функцией только от температуры, то
Δ U =∫ T 2 T 1 νCV d T.
Эта же формула верна и для вычисления изменения внутренней энергии любого тела, но только в процессах при постоянном объёме (изохорных процессах); в общем случае CV (T, V) является функцией и температуры, и объёма.
Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим:
Δ U = νCV Δ T,
где ν — количество вещества, Δ T — изменение температуры.
Для идеального газа внутренняя энергия равна:
U = i 2⋅ νRT,
где i - количество степеней свободы, R - универсальная газовая постоянная.
Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
p ⋅ VM = R ⋅ T,
где
· p — давление,
· VM — молярный объём,
· R — универсальная газовая постоянная
· T — абсолютная температура, К.
Так как VM = Vν, где ν — количество вещества, а ν = mM, где m — масса, M — молярная масса, уравнение состояния можно записать:
p ⋅ V = mMR ⋅ T.
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.
Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную r, значение которой необходимо было измерять для каждого газа:
p ⋅ V = r ⋅ T,
Менделеев же обнаружил, что r прямо пропорциональна ν, коэффициент пропорциональности R он назвал универсальной газовой постоянной.
Связь с другими законами состояния идеального газа[править | править вики-текст]
В случае постоянной массы газа уравнение можно записать в виде:
p ⋅ VT = ν ⋅ R,
p ⋅ VT =const.
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
T =const⇒ p ⋅ V =const — закон Бойля — Мариотта.
p =const⇒ VT =const — Закон Гей-Люссака.
V =const⇒ pT =const — закон Шарля (второй закон Гей-Люссака, 1808 г.)
А в форме пропорции p 1⋅ V 1 T 1= p 2⋅ V 2 T 2 этот закон удобен для расчёта перевода газа из одного состояния в другое.
С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
H2+Cl2=2HCl.
1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
N2+3H2=2NH3.
T =const⇒ p ⋅ V =const — закон Бойля — Мариотта.
Закон Бойля — Мариотта назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
p =(γ −1) ρε,
где γ — показатель адиабаты, ε — внутренняя энергия единицы массы вещества.
Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. И это обстоятельство может быть прояснено на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.
С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение P ⋅ V немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение P ⋅ V увеличивается.
Молекулярно-кинетическая теория (сокращённо МКТ) — теория, возникшая в XIX веке и рассматривающая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:
· все тела состоят из частиц: атомов, молекул и ионов;
· частицы находятся в непрерывном хаотическом движении (тепловом);
· частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.
МКТ стала одной из самых успешных физических теорий и была подтверждена целым рядом опытных фактов. Основными доказательствами положений МКТ стали:
· Диффузия
· Броуновское движение
· Изменение агрегатных состояний вещества
На основе МКТ развит целый ряд разделов современной физики, в частности, физическая кинетика и статистическая механика. В этих разделах физики изучаются не только молекулярные (атомные или ионные) системы, находящиеся не только в «тепловом» движении, и взаимодействующие не только через абсолютно упругие столкновения. Термин же молекулярно-кинетическая теория в современной теоретической физике уже практически не используется, хотя он встречается в учебниках по курсу общей физики.
p =13 m 0 nv 2. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения).
Упрощенный вывод основного уравнения МКТ
Пусть имеется N частиц массой m 0 в некотором кубическом сосуде.
Так как молекулы движутся хаотически, то события, состоящие в движении в одном из шести независимых направлений пространства, совпадающих с осями декартовой системы координат, равновероятны.
Поэтому, в каждом из этих направлении движется 16 N частиц.
Пусть все частицы обладают одинаковой скоростью v.
Каждая из частиц, сталкивающихся со стенкой, передаёт ей импульс Δ P =2 m 0 v.
Если площадь стенки S, а концентрация - n, то количество частиц, сталкивающихся со стенкой за время Δ t равно N =16 nS Δ tv.
Так как p = FS, а F =Δ P Δ tN - суммарная сила взаимодействия частиц со стенкой, то подставив соответствующие значения получим p =13 m 0 nv 2,
так как Ek ¯=12 mv 2¯, то p =23 nEk ¯
Уравнение среднеквадратичной скорости молекулы
Уравнение среднеквадратичной скорости молекулы легко выводится из основного уравнения МКТ для одного моля газа.
Ek =12 mv 2¯=32 kT,
Nam = Mr, где Mr — молярная масса газа, m — масса молекулы газа.
Отсюда окончательно
v ¯=√3 kTNA, √3 RT
Mr Mr
- основное уравнение МКТ идеального газа. Выведено в предположении, что давление газа есть результат ударов его молекул о стенки сосуда. 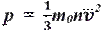 Это же уравнение в другой записи: Это же уравнение в другой записи: 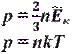 · 18. термодинамический процесс — термодинамический процесс; процесс Изменение состояния системы, характеризующееся изменением ее термодинамических параметров.
· термодинамический процесс — [thermodynamic process] процесс в макроскопической системе, связанный с переходом ее из одного равновесного состояния в другое в результате внешних воздействий. Различают следующие основные виды термодинамического процесса: адиабатный.
· термодинамический процесс — ▲ процесс ↑ теплота термодинамические процессы процессы энергетического взаимодействия вещества. расширение. < > сжатие. диссипация. экзотермический. < > эндотермический. изотонический. изоэнтропический. ↓ изотерма. изотермический
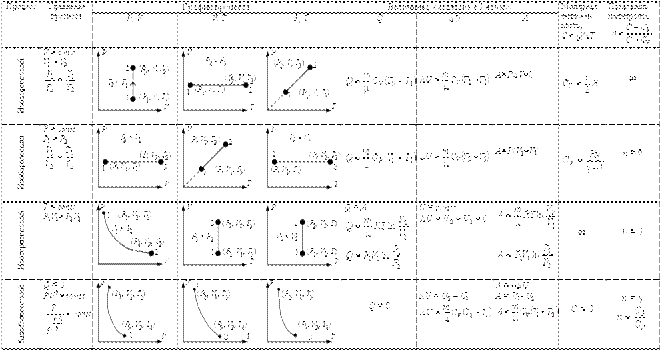
Термодинамика изучает пять основных процессов идеальных газов: изохорный, (v= const) происходящий при постоянном объеме газа; изобарный, (р = const) происходящий при постоянном давлении; изотермический, (Т = const) происходящий при постоянной температуре; адиабатный, (q = 0) протекающий без подвода или отвода теплоты, т.е. протекающий без теплообмена с окружающей средой; политропный — обобщенный процесс изменения всех параметров рабочего тела при наличии теплообмена; для него четыре предыдущих процесса являются частными случаями.
Для изучения этих процессов необходимо определить:
уравнение процесса, которое устанавливает закономерность изменения состояния рабочего тела;графическое изображение процесса в диаграммах; связь между параметрами в процессе; изменение внутренней энергии рабочего тела в процессе; работу, совершаемую рабочим телом в процессе;теплоту, участвующую в процессе.
Изохорный процесс Уравнение изохорного процесса: v = const.
Графически в p-v -диаграмме изохорный процесс изображается линией, параллельной оси давлений Линии изохорного процесса в диаграмме состояния называется изохорой
· 18. термодинамический процесс — термодинамический процесс; процесс Изменение состояния системы, характеризующееся изменением ее термодинамических параметров.
· термодинамический процесс — [thermodynamic process] процесс в макроскопической системе, связанный с переходом ее из одного равновесного состояния в другое в результате внешних воздействий. Различают следующие основные виды термодинамического процесса: адиабатный.
· термодинамический процесс — ▲ процесс ↑ теплота термодинамические процессы процессы энергетического взаимодействия вещества. расширение. < > сжатие. диссипация. экзотермический. < > эндотермический. изотонический. изоэнтропический. ↓ изотерма. изотермический
Термодинамика изучает пять основных процессов идеальных газов: изохорный, (v= const) происходящий при постоянном объеме газа; изобарный, (р = const) происходящий при постоянном давлении; изотермический, (Т = const) происходящий при постоянной температуре; адиабатный, (q = 0) протекающий без подвода или отвода теплоты, т.е. протекающий без теплообмена с окружающей средой; политропный — обобщенный процесс изменения всех параметров рабочего тела при наличии теплообмена; для него четыре предыдущих процесса являются частными случаями.
Для изучения этих процессов необходимо определить:
уравнение процесса, которое устанавливает закономерность изменения состояния рабочего тела;графическое изображение процесса в диаграммах; связь между параметрами в процессе; изменение внутренней энергии рабочего тела в процессе; работу, совершаемую рабочим телом в процессе;теплоту, участвующую в процессе.
Изохорный процесс Уравнение изохорного процесса: v = const.
Графически в p-v -диаграмме изохорный процесс изображается линией, параллельной оси давлений Линии изохорного процесса в диаграмме состояния называется изохорой
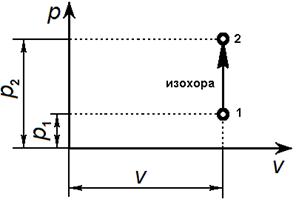 Связь между параметрами в изохорном процессе подчиняется закону Шарля
Связь между параметрами в изохорном процессе подчиняется закону Шарля
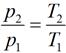 /*
/*
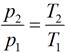 */
И изохорном процессе вся подведенная теплота расходуется на изменение внутренней энергии тела. Для тела с произвольной массой вещества m имеем:
*/
И изохорном процессе вся подведенная теплота расходуется на изменение внутренней энергии тела. Для тела с произвольной массой вещества m имеем:
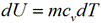
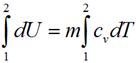 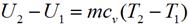 где cv — средняя массовая изохорная теплоемкость в интервале температур от T 1, до Т 2.
Теплоемкостью называется количество теплоты, которое следует подвести к единице количества вещества для нагревания его на 1 градус. Массовая теплоемкость выражается в кДж/(кг • К), объемная — в кДж/(м3 • К), мольная — в кДж/(кмоль • К).
Так как в изохорном процессе нет изменения объема, то и работа по его изменению не совершается: W1-2 = 0.
Количество теплоты, подведенное в изохорном процессе, равно изменению внутренней энергии. Для произвольной массы вещества:
где cv — средняя массовая изохорная теплоемкость в интервале температур от T 1, до Т 2.
Теплоемкостью называется количество теплоты, которое следует подвести к единице количества вещества для нагревания его на 1 градус. Массовая теплоемкость выражается в кДж/(кг • К), объемная — в кДж/(м3 • К), мольная — в кДж/(кмоль • К).
Так как в изохорном процессе нет изменения объема, то и работа по его изменению не совершается: W1-2 = 0.
Количество теплоты, подведенное в изохорном процессе, равно изменению внутренней энергии. Для произвольной массы вещества:
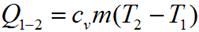 Изобарный процесс
Уравнение изобарного процесса р= const.
Графически изобарный процесс в р—v- диаграмме изображается прямой линией, параллельной оси объемов. Линия изобарного процесса называется изобарой.
Изобарный процесс
Уравнение изобарного процесса р= const.
Графически изобарный процесс в р—v- диаграмме изображается прямой линией, параллельной оси объемов. Линия изобарного процесса называется изобарой.
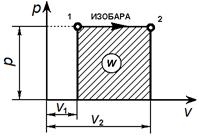 Связь между параметрами в изобарным процессе выража ется законом Гей-Люссака:
Связь между параметрами в изобарным процессе выража ется законом Гей-Люссака:
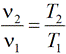 Изменение внутренней энергии газа рассчитывается по формуле:
Изменение внутренней энергии газа рассчитывается по формуле:
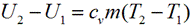 В изобарном процессе происходит изменение объема рабочего тела, следовательно, совершается работа, определяемая:
В изобарном процессе происходит изменение объема рабочего тела, следовательно, совершается работа, определяемая:

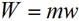 Для произвольной массы газа m формула работы примет:
Для произвольной массы газа m формула работы примет:
 где V1, V2 - объем m кг газа в начале и конце процесса, м3. Воспользовавшись первым законом термодинамики, можем рассчитать теплоту процесса (для 1 кг газа) по формуле:
где V1, V2 - объем m кг газа в начале и конце процесса, м3. Воспользовавшись первым законом термодинамики, можем рассчитать теплоту процесса (для 1 кг газа) по формуле:
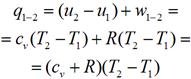 При этом в термодинамике существует связь между изохорной cv и изобарной ср теплоемкостями. Связь устанавливается уравнением Майера:
При этом в термодинамике существует связь между изохорной cv и изобарной ср теплоемкостями. Связь устанавливается уравнением Майера:
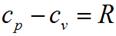 Тогда выражение для определения количества теплоты для 1 кг газа примет вид:
Тогда выражение для определения количества теплоты для 1 кг газа примет вид:
 для произвольной массы газа:
для произвольной массы газа:
 Таким образом, в изобарном процессе теплота расходуется на совершение работы и на изменение внутренней энергии рабочего тела.
Изотермический процесс
Уравнение изотермического процесса: Т= const или pv = const.Графически изотермический процесс в р—v-диаграмме изображается в виде равнобокой гиперболы что вытекает из уравнения pv = const, и называется изотермой.
Таким образом, в изобарном процессе теплота расходуется на совершение работы и на изменение внутренней энергии рабочего тела.
Изотермический процесс
Уравнение изотермического процесса: Т= const или pv = const.Графически изотермический процесс в р—v-диаграмме изображается в виде равнобокой гиперболы что вытекает из уравнения pv = const, и называется изотермой.
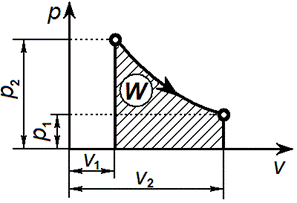 Связь между параметрами изотермического процесса определяется законом Бойля — Мариотта:
Связь между параметрами изотермического процесса определяется законом Бойля — Мариотта:
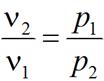 Так как Т1 = Т2, изменение внутренней энергии газа в изотермическом процессе равно нулю:
Так как Т1 = Т2, изменение внутренней энергии газа в изотермическом процессе равно нулю:
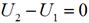 Совершенная 1 кг газа работа в изотермическом процессе, c учетом того что RT = const, определяется следующим образом:
Совершенная 1 кг газа работа в изотермическом процессе, c учетом того что RT = const, определяется следующим образом:
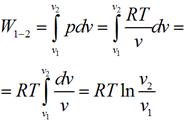 Пользуясь законом Бойля — Мариотта, получим:
Пользуясь законом Бойля — Мариотта, получим:
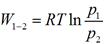 Для произвольной массы рабочего тела уравнение работы примет вид:
Для произвольной массы рабочего тела уравнение работы примет вид:
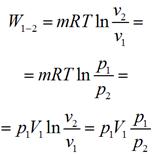 Графически в p-v диаграмме работа в процессе 1-2 определяется площадью под изотермой. Теплота, участвующая в изотермическом процессе, определится соотношением:
Графически в p-v диаграмме работа в процессе 1-2 определяется площадью под изотермой. Теплота, участвующая в изотермическом процессе, определится соотношением:
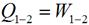 Это означает что вся подведенная в изотермическом процессе теплота расходуется на совершение работы.
Это означает что вся подведенная в изотермическом процессе теплота расходуется на совершение работы.
|
19. Вну́тренняя эне́ргия термодинамической системы (обозначается как E или U) — это сумма энергий теплового движения молекул и межмолекулярных взаимодействий. В аксиоматической термодинамике движение молекул не рассматривается, и внутренняя энергия термодинамической системы определяется как функция состояния системы, приращение которой в любом процессе для адиабатически изолированной системы равно работе внешних сил при переходе системы из начального состояния в конечное. Будучи функцией состояния, внутренняя энергия однозначно определяется состоянием системы. Изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между её значениями в конечном и начальном состояниях, независимо от предыстории системы и от пути, по которому совершался переход.Внутренняя энергия определяется с точностью до произвольной аддитивной постоянной, и её нельзя измерить напрямую. Можно определить только изменение внутренней энергии, то есть разность внутренней энергии в различных состояниях, которая не зависит от выбора произвольной постоянной.
Термодинамическое определение внутренней энергии указывает на способ измерения этой величины. В математическом выражении для первого начала термодинамики:
Δ U = δQ − δA, где
· δQ — подведённое к телу количество теплоты, измеренное в джоулях
· δA — работа, совершаемая телом против внешних сил, измеренная в джоулях
необходимо положить δQ =0 для адиабатически изолированной системы. Приняв какое-либо состояние системы за нулевое, можно измерить работу, совершаемую внешними силами при переходе из нулевого состояния в любое другое состояние (или обратно). Тем самым система будет «энергетически проградуирована», каждому её состоянию будет сопоставлено определенное значение внутренней энергии[2]. Такая система, в свою очередь, сможет служить прибором (калориметром), с помощью которого можно будет измерять изменение внутренней энергии других систем, приводимых в тепловой контакт с системой.Для квазистатических процессов выполняется следующее соотношение:
dU = TdS − pdV + μdN, где
· T — температура, измеренная в кельвинах
· S — энтропия, измеренная в джоулях/кельвин
· p — давление, измеренное в паскалях
· μ — химический потенциал
· N — количество частиц в системе
· Внутренняя энергия - это энергия системы за вычетом ее полной механической энергии (которая складывается из кинетической энергии системы как целого и ее потенциальной энергии в поле внешних сил):
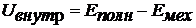
Внутренняя энергия системы складывается из:
а) кинетической энергии непрерывного хаотического движения молекул;
б) потенциальной энергии взаимодействия молекул между собой;
в) внутримолекулярной энергии (энергии химических связей, ядерной энергии и т.п.).
· Для идеального газа внутренняя энергия равна суммарной кинетической энергии хаотического движения всех N молекул газа:
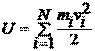 .
.
· Внутренняя энергия системы аддитивна, т.е. складывается из внутренних энергий ее частей.
· Внутренняя энергия системы является функцией состояния. Поэтому приращение внутренней энергии (как и приращение всех функций состояния) всегда будет полным дифференциалом dU.
· При циклическом процессе, когда система приходит в исходное состояние, ее внутренняя энергия не меняется.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 709; Нарушение авторских прав?; Мы поможем в написании вашей работы!