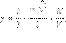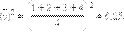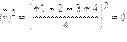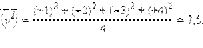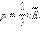Функции процесса

Параметры состояния

Поскольку функции состояния связаны между собой уравнениями состояния и другими уравнениями (например, уравнением Гиббса — Дюгема), для однозначной характеристики состояния системы оказывается достаточным знания только немногих величин, называемых независимыми переменными состояния или, более кратко, параметрами состояния термодинамической системы. Остальные термодинамические функции состояния являются математическими функциями параметров состояния и определяются однозначно, если заданы значения последних. При этом для многих задач не имеет значения, известны ли конкретные уравнения состояния изучаемой системы; важно только, что соответствующие зависимости всегда реально существуют. Число параметров состояния зависит от характера конкретной системы, а выбор их в принципе произволен и связан с соображениями целесообразности^[1].

Функции процесса зависят не только от текущего состояния системы, но также и от пути, по которому система пришла в данное состояние.

К функциям процесса в термодинамике относят

· количество теплоты Q,

· термодинамическую работу A.

Для равновесных процессов эти величины могут быть выражены через функции состояния с помощью интегрирующего множителя:

· dS = δQT, где S (энтропия) и T (абсолютная температура) — функции состояния,

Давление – это физическая величина, равная отношению перпендикулярной составляющей силы, действующей на поверхность, к площади этой поверхности.

Сила действует на стенку со стороны множества молекул. Она может быть рассчитана как произведение силы, действующей со стороны одной молекулы, на число молекул, движущихся в сосуде в направлении этой стенки. Так как пространство трехмерно и каждое измерение имеет два направления: положительное и отрицательное, можно считать, что в направлении одной стенки движется одна шестая часть всех молекул (при большом их числе): N = N ₀ / 6.

Сила, действующая на стенку со стороны одной молекулы, равна силе, действующей на молекулу со стороны стенки. Сила, действующая на молекулу со стороны стенки, равна произведению массы одной молекулы на ускорение, которое она получает при ударе о стенку:

F' = m ₀ a.

Ускорение же – это физическая величина, определяемая отношением изменения скорости ко времени, в течение которого это изменение произошло: a = Δυ / t.

Изменение скорости равно удвоенному значению скорости молекулы до удара: Δυ = –2υ.

Если молекула ведет себя подобно резиновому мячику, нетрудно представить процесс удара: молекула, ударяясь, деформируется. На процесс сжатия и разжатия затрачивается время. Пока молекула действует на стенку сосуда, о последнюю успевает удариться еще некоторое число молекул, находящихся от нее на расстояниях не дальше l = υ t. (Например, условно говоря, пусть молекулы имеют скорость 100 м/с. Удар длится 0,01 с. Тогда за это время до стенки успеют долететь и внести свой вклад в давление молекулы, находящиеся от нее на расстояниях 10, 50, 70 см, но не далее 100 см).

Будем рассматривать объем сосуда V = lS.

Подставив все формулы в исходную, получаем уравнение:

где: – масса одной молекулы, – среднее значение квадрата скорости молекул, N – число молекул в объеме V.

Сделаем некоторые пояснения по поводу одной из величин, входящих в полученное уравнение.

Так как движение молекул хаотично и преимущественного движения молекул в сосуде нет, их средняя скорость равна нулю. Но ясно, что это не относится к каждой отдельной молекуле.

Для вычисления давления идеального газа на стенку сосуда используется не среднее значение x -компоненты скорости молекул 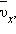а среднее значение квадрата скорости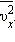

Чтобы введение этой величины было более понятным, рассмотрим численный пример.

Пусть четыре молекулы имеют скорости 1, 2, 3, 4 усл. ед.

Квадрат среднего значения скорости молекул равен:

Среднее значение квадрата скорости равно:

Если скорости молекул равны +1, –2, –3, +4 усл. ед., то квадрат среднего значения скорости равен:

Среднее значение квадрата скорости равно:

Средние значения проекций квадрата скорости на оси x, y, z связаны со средним значением квадрата скорости соотношением:

Если извлечь квадратный корень из то получим величину, которая называется средней квадратичной скоростью молекул.

Величина, определяемая отношением числа частиц к объему, в котором они находятся, называется концентрацией (обозначается буквой n).

Величина же – это средняя кинетическая энергия каждой молекулы газа.

С учетом этого полученное уравнение можно переписать в виде:

Уравнения связывают макропараметры газа – его давление и объем (p, V) с микропараметрами – массой молекул и их скоростью (m ₀, υ), или энергией

Последнее уравнение читается следующим образом: давление идеального газа на стенки сосуда прямо пропорционально концентрации молекул в сосуде и их средней кинетической энергии.

давление газа — статическое давление движущегося газа относительно атмосферного давления. Единица физической величины килопаскаль (кПа). (Смотри: ГОСТ Р 51733 2001. Котлы газовые центрального отопления, оснащенные атмосферными горелками, номинальной тепловой. Давление газа. Мы уже знаем, что газы, в отличии от твердых тел и жидкостей, заполняют весь предоставленный им объем, например стальной баллон для хранения газом, камеру автомобильной шины или волейбольного мяча. При этом газ оказывает оказывает давление на стенки, дно и крышку баллона, камеры или любого другого тела в котором он находится. Давление газа обусловлено иными причинами, чем давление твердого тела на опору. Известно, что молекулы газа беспорядочно движутся. При своем движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ. Молекул в газе много, поэтому число их ударов очень велико. Хотя сила удара отдельной молекулы мала, но действие всех молекул о стенки сосуда значительно, оно и создает давление газ.Итак, давление газа вызывается ударами молекул на стенки сосуда. Температу́ра (от лат. temperatura — надлежащее смешение, нормальное состояние) — скалярная физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Температура всех частей системы, находящейся в равновесии, одинакова. Если система не находится в равновесии, то между её частями, имеющими различную температуру, происходит теплопередача (переход энергии от более нагретых частей системы к менее нагретым), приводящая к выравниванию температур в системе.Температура определяет: распределение образующих систему частиц по уровням энергии (см. Статистика Максвелла — Больцмана) и распределение частиц по скоростям (см. Распределение Максвелла); степень ионизации вещества (см. Уравнение Саха); спектральную плотность излучения (см. Формула Планка); полную объёмную плотность излучения (см. Закон Стефана — Больцмана) и т. д. Температуру, входящую в качестве параметра в распределение Больцмана, часто называют температурой возбуждения, в распределение Максвелла — кинетической температурой, в формулу Саха — ионизационной температурой, в закон Стефана — Больцмана — радиационной температурой. Поскольку для системы, находящейся в термодинамическом равновесии, все эти параметры равны друг другу, их называют просто температурой системы^. Температура относится к интенсивным величинам, не зависящим от массы системы.Более строгие определения температуры, даваемые ей в различных разделах физики, смотри ниже.Интуитивно понятие температура появилось как мера градации наших ощущений тепла и холода; на бытовом уровне температура воспринимается как параметр, служащий для количественного описания степени нагретости материального объекта^.

Среднемесячные температуры поверхности с 1961 по 1990 годы

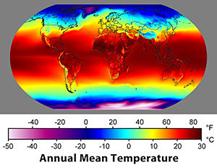
Среднегодовая температура по всему миру

Тепловое движение α-пептида. Сложное колебательное движение атомов, составляющих пептид, случайно, и энергия отдельного атома флуктуирует в широких пределах, но с помощью закона равнораспределения вычисляют как среднюю кинетическую энергию каждого атома, так и среднюю потенциальную энергию многих колебаний. Серые, красные и синие шары обозначают атомы углерода, кислорода иазота, соответственно; маленькие белые шарики представляют атомы водорода.

В Международной системе величин (англ. International System of Quantities, ISQ) термодинамическая температура выбрана в качестве одной из семи основных физических величин системы. Соответственно, вМеждународной системе единиц (СИ), основанной на Международной системе величин, единица этой температуры — кельвин — является одной из семи основных единиц СИ^. Кроме термодинамической температуры в СИ используется температура Цельсия, её единицей является градус Цельсия, входящий в состав производных единиц СИ, имеющих специальные наименования и обозначения, и по размеру равный кельвину^[4]. На практике часто применяют градусы Цельсия из-за исторической привязки к важным характеристикам воды — температуре таяния льда (0 °C) и температуре кипения (100 °C). Это удобно, так как большинство климатических процессов, процессов в живой природе и т. д. связаны с этим диапазоном. Изменение температуры на один градус Цельсия тождественно изменению температуры на один кельвин. Поэтому после введения в 1967 г. нового определения кельвина, температура кипения воды перестала играть роль неизменной реперной точки и, как показывают точные измерения, она уже не равна 100 °C, а близка к 99,975 °C^[2].Существуют также шкала Фаренгейта и некоторые другие.

Дата добавления: 2014-11-08